题目内容
13.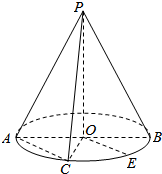 如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,
如图,圆锥的顶点为P,底面圆为O,底面的一条直径为AB,C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,已知PO=2,OA=1,(1)求三棱锥P-AOC的体积;
(2)求异面直线PA和OE所成角的余弦值.
分析 (1)由条件便知PO为三棱锥P-AOC的高,底面积S△AOC又容易得到,从而带入棱锥的体积公式即可得到该三棱锥的体积.
(2)根据条件能够得到OE∥AC,从而找到异面直线PA,OE所成角为∠PAC,可取AC中点H,连接PH,便得到PH⊥AC,从而可在Rt△PAH中求出cos∠PAC.
解答 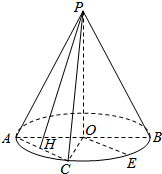 解:(1)∵PO=2,OA=1,OC⊥AB,
解:(1)∵PO=2,OA=1,OC⊥AB,
∴三棱锥P-AOC的体积V=$\frac{1}{3}×\frac{1}{2}×1×1×2$=$\frac{1}{3}$;
(2)∵C为半圆弧$\widehat{AB}$的中点,E为劣弧$\widehat{CB}$的中点,
∴∠BOE=45°,又∠ACO=45°;
∴OE∥AC;
∴∠PAC便是异面直线PA和OE所成角;
在△ACP中,AC=$\sqrt{2}$,AP=CP=$\sqrt{5}$.
如图,取AC中点H,连接PH,则PH⊥AC,AH=$\frac{\sqrt{2}}{2}$
∴在Rt△PAH中,cos∠PAH=$\frac{{\sqrt{10}}}{10}$;
∴异面直线PA与OE所成角的余弦值为$\frac{{\sqrt{10}}}{10}$.
点评 考查圆锥的定义,圆锥的高和母线,等弧所对的圆心角相等,能判断两直线平行,以及异面直线所成角的定义及找法、求法,属于中档题.

练习册系列答案
相关题目
1.定义移动运算“⊕”,对于任意正整数n满足以下运算:(1)1⊕1=1;(2)(n+1)⊕1=2+n⊕1,则n⊕1用含n的代数式可表示为( )
| A. | 2n-1 | B. | n | C. | 2n-1 | D. | 2n-1 |
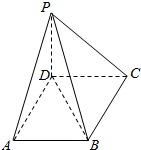 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥底面ABCD,AB=2AD,∠ADB=90°,
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PD⊥底面ABCD,AB=2AD,∠ADB=90°,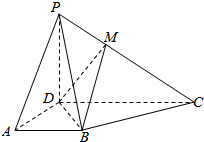 如图所示,已知ABCD为梯形,AB∥CD,CD=2AB,且PD⊥平面ABCD,M为线段PC上一点.
如图所示,已知ABCD为梯形,AB∥CD,CD=2AB,且PD⊥平面ABCD,M为线段PC上一点.