题目内容
已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线上。
(1)求动点M的轨迹方程;
(2)设过定点F,法向量 =(4,-3)的直线与(1)中的轨迹相交于A,B两点,判断
=(4,-3)的直线与(1)中的轨迹相交于A,B两点,判断 能否为钝角并说明理由。
能否为钝角并说明理由。
(1)求动点M的轨迹方程;
(2)设过定点F,法向量
 =(4,-3)的直线与(1)中的轨迹相交于A,B两点,判断
=(4,-3)的直线与(1)中的轨迹相交于A,B两点,判断 能否为钝角并说明理由。
能否为钝角并说明理由。
解:(1)动点M到定点F(1,0)的距离与到定直线l:x=-1:的距离相等,所以M的轨迹是以点f为焦点,直线l为准线的抛物线,轨迹方程为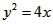 ;
;
(2)由题意,直线AB的方程为4x-3y-4=0
故A、B两点的坐标满足方程组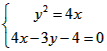
得A(4,4),B(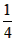 ,-1)
,-1)
设C(-1,y),则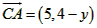 ,
,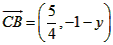
由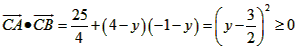 ,所以
,所以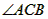 不可能为钝角。
不可能为钝角。

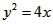 ;
;(2)由题意,直线AB的方程为4x-3y-4=0
故A、B两点的坐标满足方程组
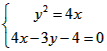
得A(4,4),B(
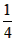 ,-1)
,-1) 设C(-1,y),则
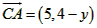 ,
,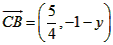
由
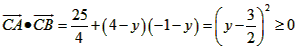 ,所以
,所以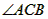 不可能为钝角。
不可能为钝角。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
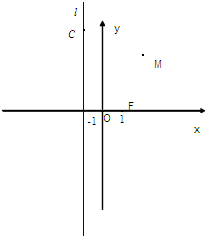 已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.
已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.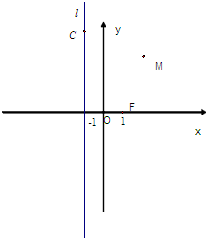 已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.
已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.