题目内容
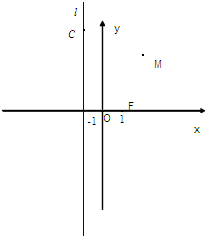 已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.
已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.(1)求动点M的轨迹方程;
(2)设过定点F,法向量
| n |
分析:(1)动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,由此能求出M的轨迹方程.
(2)直线AB的方程为4x-3y-4=0,故A、B两点的坐标满足方程组
,得A(4,4),B(
,-1)
设C(-1,y),则
=(5,4-y),
=(
,-1-y),由此知∠ACB不可能为钝角.
(2)直线AB的方程为4x-3y-4=0,故A、B两点的坐标满足方程组
|
| 1 |
| 4 |
设C(-1,y),则
| CA |
| CB |
| 5 |
| 4 |
解答: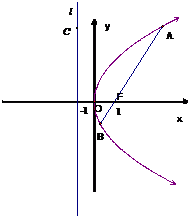 解:(1)动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,
解:(1)动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,
所以M的轨迹是以点F为焦点,直线l为准线的抛物线,
轨迹方程为y2=4x(6分)
(2)由题意,直线AB的方程为4x-3y-4=0(8分)
故A、B两点的坐标满足方程组
得A(4,4),B(
,-1)
设C(-1,y),则
=(5,4-y),
=(
,-1-y)(10分)
由
•
=
+(4-y)(-1-y)=(y-
)2≥0,
所以∠ACB不可能为钝角.(13分)
 解:(1)动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,
解:(1)动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,所以M的轨迹是以点F为焦点,直线l为准线的抛物线,
轨迹方程为y2=4x(6分)
(2)由题意,直线AB的方程为4x-3y-4=0(8分)
故A、B两点的坐标满足方程组
|
得A(4,4),B(
| 1 |
| 4 |
设C(-1,y),则
| CA |
| CB |
| 5 |
| 4 |
由
| CA |
| CB |
| 25 |
| 4 |
| 3 |
| 2 |
所以∠ACB不可能为钝角.(13分)
点评:本题考查轨迹方程的求法和判断∠ACB能否为钝角并说明理由.解题时要认真审题,熟练掌握抛物线的性质,合理地进行等价转化.

练习册系列答案
相关题目
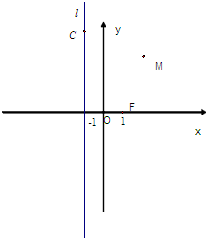 已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.
已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.