题目内容
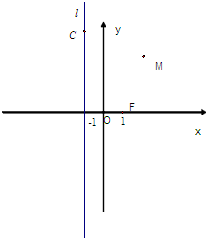 已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.
已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.(1)求动点M的轨迹方程;
(2)设过定点F,法向量
| n |
分析:(1)根据抛物线的定义一动点M到定点的距离与到定直线的距离相等,M的轨迹为抛物线,可知M的轨迹是以点F为焦点,直线l为准线的抛物线,根据F的坐标求出p的值,即可确定出抛物线的方程;
(2)根据已知的法向量得到直线AB方程的斜率,再由F的坐标即可写出直线AB的方程,与(1)求出的抛物线方程联立,求出x与y的值,确定出点A和点B的坐标,设出点C的坐标,进而表示出
h和
,利用平面向量的数量积的运算法则表示出两向量的数量积,变形后得到其数量积大于等于0,故∠ACB不可能为钝角;表示出过点B与直线AB的直线,令x=-1求出此时y的值,则y小于求出的值即可得到∠ABC为钝角时点C纵坐标的取值范围.
(2)根据已知的法向量得到直线AB方程的斜率,再由F的坐标即可写出直线AB的方程,与(1)求出的抛物线方程联立,求出x与y的值,确定出点A和点B的坐标,设出点C的坐标,进而表示出
| CA |
| CB |
解答: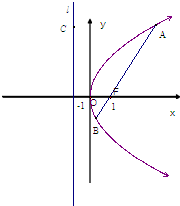 解:(1)因为动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,
解:(1)因为动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,
所以M的轨迹是以点F为焦点,直线l为准线的抛物线,
则轨迹方程为y2=4x;(4分)
(2)由题意,直线AB的方程为4x-3y-4=0(5分)
故A、B两点的坐标满足方程组
,
解得A(4,4),B(
,-1),
设C(-1,y),则
=(5,4-y),
=(
,-1-y),(8分)
由
•
=
+(4-y)(-1-y)=(y-
)2≥0,
所以∠ACB不可能为钝角.(10分)
过B垂直于直线AB的直线方程为3x+4y+
=0,
令x=-1,解得y=-
,
当∠ABC为钝角时,点C纵坐标的取值范围是:y<-
(y≠-
).(13分)
 解:(1)因为动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,
解:(1)因为动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,所以M的轨迹是以点F为焦点,直线l为准线的抛物线,
则轨迹方程为y2=4x;(4分)
(2)由题意,直线AB的方程为4x-3y-4=0(5分)
故A、B两点的坐标满足方程组
|
解得A(4,4),B(
| 1 |
| 4 |
设C(-1,y),则
| CA |
| CB |
| 5 |
| 4 |
由
| CA |
| CB |
| 25 |
| 4 |
| 3 |
| 2 |
所以∠ACB不可能为钝角.(10分)
过B垂直于直线AB的直线方程为3x+4y+
| 13 |
| 4 |
令x=-1,解得y=-
| 1 |
| 16 |
当∠ABC为钝角时,点C纵坐标的取值范围是:y<-
| 1 |
| 16 |
| 8 |
| 3 |
点评:本题考查抛物线的定义与应用,及轨迹方程的求法,关键是看清题中给出的条件,灵活运用平面向量的数量积的运算法则进行求解.本题容易忽略y≠-
的情况.
| 8 |
| 3 |

练习册系列答案
相关题目
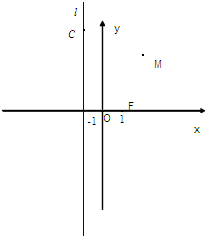 已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.
已知动点M到定点F(1,0)的距离与到定直线l:x=-1的距离相等,点C在直线l上.