题目内容
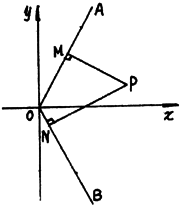
已知：如图，射线OA为y＝2x(x＞0)，射线OB为y＝－2x(x＞0)，动点P(x，y)在∠AOx的内部，PM⊥OA于M，PN⊥OB于N，四边形ONPM的面积为2．
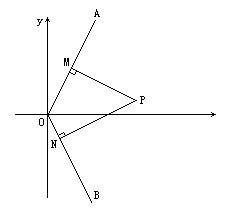
(Ⅰ)动点P的纵坐标y是其横坐标x的函数，求这个函数y＝f(x)的解析式；
(Ⅱ)确定y＝f(x)的定义域．
答案：
解析：
解析：
|
解：(Ⅰ)设M(a，2a)，N(b，－2b)(a＞0，b＞0) 则|OM|＝ 由动点P在∠AOx的内部，得O＜y＜2x．
＝ ∴2(a＋b)x－(a－b)y＝4 ①
代入①式消去a、b，并化简得 ∵y＞0，∴y＝ (Ⅱ)由P在∠AOx内部，得O＜y＜2x． 又垂足N必须在射线OB上，否则O、N、P、M四点不能构成四边形，所以还必须满足条件y＜
所以y＝f(x)的定义域为 |
a，|ON|＝
[2(a＋b)x－(a－b)y]＝2
＝5．
练习册系列答案
相关题目
如图，已知：射线OA为y=kx（k＞0，x＞0），射线OB为y=-kx（x＞0），动点P（x，y）在∠AOx的内部，PM⊥OA于M，PN⊥OB于N，四边形ONPM的面积恰为k．
已知正三棱柱ABC-A′B′C′的正（主）视图和侧（左）视图如图所示．设△ABC，△A′B′C′的中心分别是O，O′，现将此三棱柱绕直线OO′旋转，射线OA旋转所成的角为x弧度（x可以取到任意一个实数），对应的俯视图的面积为S（x），则函数S（x）的最大值为
的内部，
于N，四边形ONPM的面积为2..