题目内容
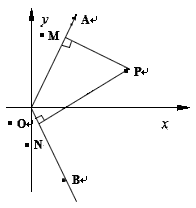
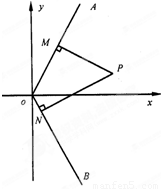
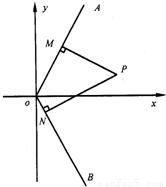
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.(1)设M(a,ka),N(b,-kb),(a>0,b>0),求P(x,y)(x>0,0<y<kx)分别到直线OM,ON的距离.
(2)当k为定值时,动点P的纵坐标y是横坐标x的函数,求这个函数y=f(x)的解析式;
(3)根据k的取值范围,确定y=f(x)的定义域.
分析:(1)先要仔细分析题目所给的条件,设出点M、N的坐标,代入点到直线距离公式,可求出点P到直线OM,ON的距离.
(2)将四边形分解成两个三角形:三角形OMP、三角形ONP分别表示出面积,然后求和即可找到x、y之间的关系式,进而即可获得问题的解答;
(3)首先由0<y<kx,得到x必须的范围,然后根据k分类讨论,同时注意要构成四边形的隐含条件,进而即可获得自变量x的范围,最后注意分情况下结论,进而问题即可获得解答.
(2)将四边形分解成两个三角形:三角形OMP、三角形ONP分别表示出面积,然后求和即可找到x、y之间的关系式,进而即可获得问题的解答;
(3)首先由0<y<kx,得到x必须的范围,然后根据k分类讨论,同时注意要构成四边形的隐含条件,进而即可获得自变量x的范围,最后注意分情况下结论,进而问题即可获得解答.
解答:解:(1)设M(a,ka),N(b,-kb),(a>0,b>0).
则|OM|=a
,|ON|=b
.
(2)由动点P在∠AOx的内部,得0<y<kx.
∴|PM|=
=
,|PN|=
=
∴S四边形ONPM=S△ONP+S△OPM=
(|OM|•|PM|+|ON|•|PN|)
=
[a(kx-y)+b(kx+y)]=
[k(a+b)x-(a-b)y]=k
∴k(a+b)x-(a-b)y=2k①
又由kPM=-
=
,kPN=
=
,
分别解得a=
,b=
,代入①式消a、b,并化简得x2-y2=k2+1.
∵y>0,
∴y=
(3)由0<y<kx,得0<
<kx?0<x2-k2-1<k2x2?(1-k2)x2<k2+1<x(*)
当k=1时,不等式②为0<2恒成立,∴(*)?x>
.
当0<k<1时,由不等式②得x2<
,x<
,
∴(*)?
<x<
.
当k>1时,由不等式②得x2>
,且
<0,
∴(*)?x>
但垂足N必须在射线OB上,否则O、N、P、M四点不能组成四边形,所以还必须满足条件:y<
x,将它代入函数解析式,得
<
x
解得
<x<
(k>1),或x∈k(0<k≤1).
综上:当k=1时,定义域为{x|x>
};
当0<k<1时,定义域为{x|
<x<
};
当k>1时,定义域为{x|
<x<
}.
则|OM|=a
| 1+k2 |
| 1+k2 |
(2)由动点P在∠AOx的内部,得0<y<kx.
∴|PM|=
| |kx-y| | ||
|
| kx-y | ||
|
| |kx+y| | ||
|
| kx+y | ||
|
∴S四边形ONPM=S△ONP+S△OPM=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
∴k(a+b)x-(a-b)y=2k①
又由kPM=-
| 1 |
| k |
| y-ka |
| x-a |
| 1 |
| k |
| y+kb |
| x-b |
分别解得a=
| x+ky |
| 1+k2 |
| x-ky |
| 1+k2 |
∵y>0,
∴y=
| x2-k2-1 |
(3)由0<y<kx,得0<
| x2-k2-1 |
当k=1时,不等式②为0<2恒成立,∴(*)?x>
| 2 |
当0<k<1时,由不等式②得x2<
| k2+1 |
| 1-k2 |
| ||
| 1-k2 |
∴(*)?
| 1+k2 |
| ||
| 1-k2 |
当k>1时,由不等式②得x2>
| k2+1 |
| 1-k2 |
| k2+1 |
| 1-k2 |
∴(*)?x>
| 1+k2 |
但垂足N必须在射线OB上,否则O、N、P、M四点不能组成四边形,所以还必须满足条件:y<
| 1 |
| k |
| x2-k2-1 |
| 1 |
| k |
解得
| 1+k2 |
k
| ||
| k2-1 |
综上:当k=1时,定义域为{x|x>
| 2 |
当0<k<1时,定义域为{x|
| 1+k2 |
| ||
| 1-k2 |
当k>1时,定义域为{x|
| 1+k2 |
k
| ||
| k2-1 |
点评:本题考查的是函数解析式的求解和定义域的求解的综合类问题.在解答的过程当中充分体现了图形分割的思想、分类讨论的思想以及问题转化的思想.值得同学们体会和反思.

练习册系列答案
相关题目
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.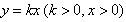 ,射线OB为
,射线OB为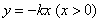 ,动点P(x,y)在
,动点P(x,y)在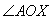 的内部,
的内部,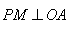 于M,
于M,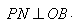 于N,四边形ONPM的面积恰为k.
于N,四边形ONPM的面积恰为k.