题目内容
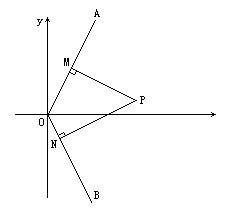
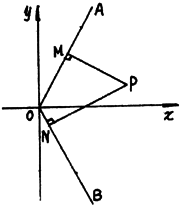
已知:如图射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.

(Ⅰ)当k为定值时,动点P的纵坐标y是其横坐标x的函数,求这个函数y=f(x)的解析式;
(Ⅱ)根据k的取值范围,确定y=f(x)的定义域.
答案:
解析:
解析:
|
解:(Ⅰ)设M(a,ka),N(b,-kb)(a>0,b>0). 则|OM|=a 由动点P在∠AOx的内部,得O<y<kx.
∴k(a+b)x-(a-b)y=2k①
分别解得 代入①式消去a、b并化简得 ∵y>0,∴y= (Ⅱ)由0<y<kx,得
当k=1时,不等式②为0<2,恒成立.
当k>1时,由不等式②得
但垂足N必须在射线OB上,否则O、N、P、M四点不能组成四边形,所以还必须满足条件 y<
解得 综上:当k=1时,定义域为{x|x> 当0<k<1时,定义域为 当k>1时,定义域为 |

练习册系列答案
相关题目
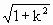 ,|ON|=b
,|ON|=b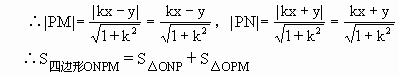

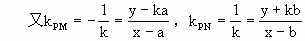

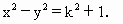
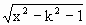
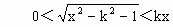
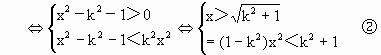
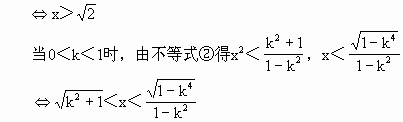
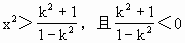
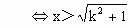
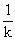 x,将它代入函数解析式,得
x,将它代入函数解析式,得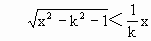
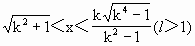
 };
};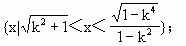
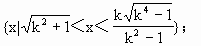
 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k. 如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.
如图,已知:射线OA为y=kx(k>0,x>0),射线OB为y=-kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k.