题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,函数
时,函数![]() 的图象恒不在
的图象恒不在![]() 轴的上方,求实数
轴的上方,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)对函数求导,对参数![]() 分类讨论,利用导数的正负求得函数的单调区间;(2)将问题转化为
分类讨论,利用导数的正负求得函数的单调区间;(2)将问题转化为![]() ,由
,由![]() 得
得![]() ,令
,令![]() ,则
,则![]() ,对参数
,对参数![]() 分类讨论,分别求得函数
分类讨论,分别求得函数![]() 的最大值,利用函数
的最大值,利用函数![]() 的最大值不小于零,求得参数
的最大值不小于零,求得参数![]() 的取值范围.
的取值范围.
试题解析:(1) ![]() 的定义域为
的定义域为![]()
①当![]() 时,则
时,则![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,则由
时,则由![]() 知
知![]() ,由
,由![]() 知
知![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
综上,当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ,
,
当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由题意知: ![]() 恒成立,
恒成立,
而![]() 0
0![]() 0
0![]() ,
,
由![]() ,得:
,得: ![]() .
.
令![]() ,则
,则![]() ,
,
①若![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
,
从而![]() ,不符合题意;
,不符合题意;
②若![]() ,当
,当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
从而![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,
,
从而在![]() 上
上![]() ,不符合题意;
,不符合题意;
③若![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上单调递减,
上单调递减, ![]() ,
,
从而![]() 在
在![]() 上单调递减,
上单调递减, ![]() ,
,
所以![]() 恒成立,综上所述,
恒成立,综上所述, ![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
【题目】设某校新、老校区之间开车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为
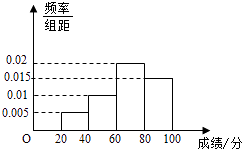
只与道路畅通状况有关,对其容量为![]() 的样本进行统计,结果如图:
的样本进行统计,结果如图:
| 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.