题目内容
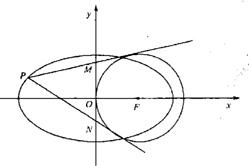 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆方程;
(2)过所求椭圆上的动点P作圆的两条切线分别交y轴于M(0,m),N(0,n)两点,当|m-n|=2
|
分析:(1)先利用圆心坐标求出焦点坐标以及c值,再利用离心率求出a,即可求出椭圆方程.
(2)先利用条件求出直线PM的方程,再利用直线PM与圆相切求出m与点P坐标之间的关系,同样求出n与点P坐标之间的关系,再把所求代入已知并利用点P在椭圆上,可以求出点P的坐标.
(2)先利用条件求出直线PM的方程,再利用直线PM与圆相切求出m与点P坐标之间的关系,同样求出n与点P坐标之间的关系,再把所求代入已知并利用点P在椭圆上,可以求出点P的坐标.
解答:解:(1)因为圆(x-1)2+y2=1的圆心是(1,0),
所以椭圆
+
=1 (a>b>0)的右焦点为F(1,0),
∴椭圆的离心率是
,
∴
=
∴a2=2,b2=1,所以椭圆方程为
+y2=1.(4分)
(2)设P(x0,y0),
由
,
得x=2-
或x=2+
(舍),
∴x0∈[-
,0)∪(0,2-
).(5分)
直线PM的方程:y-m=
x,
化简得(y0-m)x-x0y+x0m=0.
又圆心F(1,0)到直线PM的距离为1,
∴
=1
∴(y0-m)2+x02=(y0-m)2+2x0m(y0-m)+x02m2
化简得:(x0-2)m2+2y0m-x0=0,(7分)
同理:(x0-2)n2+2y0n-x0=0m+n=-
,m•n=
(9分)
∴|m-n|=
=
=
∵P(x0,y0)在椭圆上∴
+y02=1
∴|m-n|=
=2
,(11分)
∴2-
=4(
-1),∴x0=4+
(舍)或x0=-
∴P(-
,0)
所以,此时点P的坐标是(-
,0).(12分).
所以椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴椭圆的离心率是
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
∴a2=2,b2=1,所以椭圆方程为
| x2 |
| 2 |
(2)设P(x0,y0),
由
|
得x=2-
| 2 |
| 2 |
∴x0∈[-
| 2 |
| 2 |
直线PM的方程:y-m=
| y0-m |
| x0 |
化简得(y0-m)x-x0y+x0m=0.
又圆心F(1,0)到直线PM的距离为1,
∴
| |y0-m+x0m| | ||
|
∴(y0-m)2+x02=(y0-m)2+2x0m(y0-m)+x02m2
化简得:(x0-2)m2+2y0m-x0=0,(7分)
同理:(x0-2)n2+2y0n-x0=0m+n=-
| 2y0 |
| x0-2 |
| -x0 |
| x0-2 |
∴|m-n|=
| (m-n)2 |
| (m+n)2-4mn |
|
∵P(x0,y0)在椭圆上∴
| x02 |
| 2 |
∴|m-n|=
2-
|
|
∴2-
| 4 |
| (x0-2)2 |
| 2 |
| 2 |
| 2 |
| 2 |
所以,此时点P的坐标是(-
| 2 |
点评:本题的易错点在与忘记看点P所在位置,而把两个结果都要.

练习册系列答案
相关题目
 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆