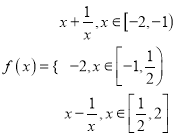题目内容
【题目】已知定义在![]() 上的函数
上的函数![]() 的导函数为
的导函数为![]() ,且
,且![]() ,若存在实数
,若存在实数![]() ,使不等式
,使不等式![]() 对于任意
对于任意![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是()
的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
对函数求导,分别求出![]() 和
和![]() 的值,得到
的值,得到![]() ,利用导数得函数
,利用导数得函数![]() 的最小值为1,把存在实数
的最小值为1,把存在实数![]() ,使不等式
,使不等式![]() 对于任意
对于任意![]() 恒成立的问题转化为
恒成立的问题转化为![]() 对于任意
对于任意![]() 恒成立,分离参数
恒成立,分离参数![]() ,分类讨论
,分类讨论![]() 大于零,等于零,小于零的情况,从而得到
大于零,等于零,小于零的情况,从而得到![]() 的取值范围。
的取值范围。
由题可得![]() ,分别把
,分别把![]() 和
和![]() 代入
代入![]() 与
与![]() 中得到
中得到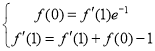 ,解得:
,解得:![]() ;
;
![]()
![]() ,
,![]() ,即
,即![]()
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
![]()
![]()
要存在实数![]() ,使不等式
,使不等式![]() 对于任意
对于任意![]() 恒成立,则不等式
恒成立,则不等式![]() 对于任意
对于任意![]() 恒成立,即不等式
恒成立,即不等式![]() 对于任意
对于任意![]() 恒成立;
恒成立;
(1)当![]() 时,显然不等式不成立,舍去;
时,显然不等式不成立,舍去;
(2)当![]() 时,不等式
时,不等式![]() 对于任意
对于任意![]() 恒成立转化为
恒成立转化为![]() 对于任意
对于任意![]() 恒成立,即
恒成立,即![]() ,解得:
,解得:![]() ;
;
(3)当![]() 时,不等式
时,不等式![]() 对于任意
对于任意![]() 恒成立转化为
恒成立转化为![]() 对于任意
对于任意![]() 恒成立,即
恒成立,即![]() ,解得:
,解得:![]() ;
;
综述所述,实数![]() 的取值范围是
的取值范围是![]()
故答案选C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
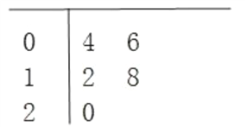
【题目】下表表示的是某款车的车速与刹车距离的关系,试分别就![]() ,
,![]() ,
,![]() 三种函数关系建立数学模型,并探讨最佳模拟,根据最佳模拟求车速为120km/h时的刹车距离.
三种函数关系建立数学模型,并探讨最佳模拟,根据最佳模拟求车速为120km/h时的刹车距离.
车速/(km/h) | 10 | 15 | 30 | 40 | 50 |
刹车距离/m | 4 | 7 | 12 | 18 | 25 |
车速/((km/h) | 60 | 70 | 80 | 90 | 100 |
刹车距离/m | 34 | 43 | 54 | 66 | 80 |