题目内容
定义在R上的函数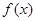 满足
满足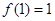 ,且对任意
,且对任意 都有
都有 ,则不等式
,则不等式 的解集为( )
的解集为( )
| A.(1,2) | B.(0,1) | C.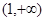 | D.(-1,1) |
D
解析试题分析:设 =
=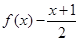 ,则
,则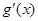 =
=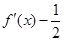 ,因为任意
,因为任意 都有
都有 ,所以任意
,所以任意 都有
都有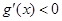 ,所以
,所以 在R上是减函数,所以
在R上是减函数,所以 等价于
等价于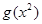 =
=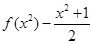 >0=
>0=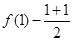 =
=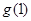 ,所以
,所以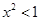 ,解得-1<
,解得-1< <1,故选D.
<1,故选D.
考点:导数与函数单调性关系,函数不等式,转化与化归思想

练习册系列答案
相关题目
已知函数 在
在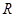 上可导,且
上可导,且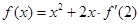 ,则函数
,则函数 的解析式为( )
的解析式为( )
A.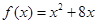 | B.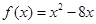 |
C.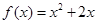 | D.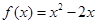 |
已知函数 在区间
在区间 上单调递减,则
上单调递减,则 的最大值是( )
的最大值是( )
A. | B. | C. | D. |
已知函数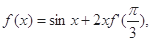 则
则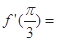 ( )
( )
A.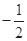 | B. | C.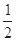 | D.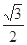 |
函数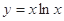 的单调递减区间是( ).
的单调递减区间是( ).
A.(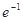 ,+∞) ,+∞) | B.(-∞,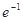 ) ) | C.(0,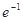 ) ) | D.(e,+∞) |
定义在R上的函数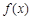 ,若对任意
,若对任意 ,都
,都
有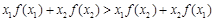 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:① ;②
;② ;③
;③ ;④
;④ 其中是“H函数”的个数为( ).
其中是“H函数”的个数为( ).
| A.4 | B.3 | C.2 | D.1 |
已知可导函数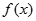 为定义域上的奇函数,
为定义域上的奇函数,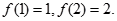 当
当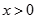 时,有
时,有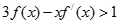 ,则
,则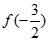 的取值范围为( )
的取值范围为( )
A.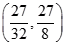 | B.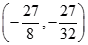 | C.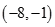 | D.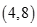 |
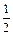 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?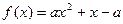 (
(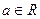 )
)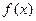 有最大值
有最大值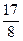 ,求实数a的值; (2)解不等式
,求实数a的值; (2)解不等式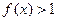 (a∈R).
(a∈R).