题目内容
直线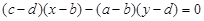
与曲线
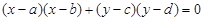的交点个数是 ．
2个
解析试题分析：通过观察方程形式，曲线是圆的方程，直线与圆最多有两个交点，而点
既满足直线，又满足曲线方程，所以有两个交点.
考点：直线与曲线的交点问题
练习册系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
假期作业暑假成长乐园新疆青少年出版社系列答案题目内容
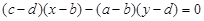直线与曲线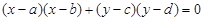的交点个数是 ．
2个
解析试题分析：通过观察方程形式，曲线是圆的方程，直线与圆最多有两个交点，而点既满足直线，又满足曲线方程，所以有两个交点.
考点：直线与曲线的交点问题
假期作业暑假成长乐园新疆青少年出版社系列答案
的抛物线的标准方程是 .
中，已知双曲线
：
（
）的一条渐近线与直线
：
垂直，则实数
．
的渐近线方程为____________________.
上的任意一点，若∠PF1F2=α，∠PF2F1=β，且cosα=
，sin(α+β)=
，则此椭圆的离心率为 ．
＋
＝1的弦被点(4,2)平分，则此弦所在直线的斜率为________．
＝1上的任意一点，F1、F2是它的两个焦点，O为坐标原点，有一动点Q满足
＝
＋
，则动点Q的轨迹方程是________．
＝1(a>b>0)的左、右焦点分别为F1，F2，线段F1F2被抛物线y2＝2bx的焦点分成5∶3两段，则此双曲线的离心率为________．