题目内容
(本题满分14分)已知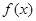 为定义在
为定义在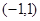 上的奇函数,当
上的奇函数,当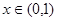 时,
时,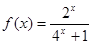 ;
;
(1)求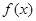 在
在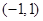 上的解析式;
上的解析式;
(2)试判断函数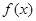 在区间
在区间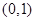 上的单调性,并给出证明.
上的单调性,并给出证明.
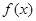 为定义在
为定义在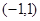 上的奇函数,当
上的奇函数,当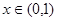 时,
时,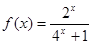 ;
;(1)求
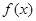 在
在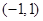 上的解析式;
上的解析式;(2)试判断函数
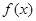 在区间
在区间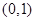 上的单调性,并给出证明.
上的单调性,并给出证明.(1) (2)函数
(2)函数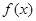 在区间
在区间 上为单调减函数,证明见解析
上为单调减函数,证明见解析
 (2)函数
(2)函数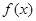 在区间
在区间 上为单调减函数,证明见解析
上为单调减函数,证明见解析试题分析:(1)当
 时,
时, ,
,所以
 ,
,又
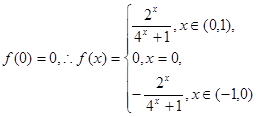 ……6分
……6分(2)函数
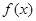 在区间
在区间 上为单调减函数.
上为单调减函数. 证明:设
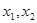 是区间
是区间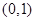 上的任意两个实数,且
上的任意两个实数,且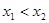 ,
,则
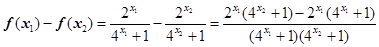
 ,
,因为
 ,
,所以
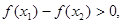 即
即 .
. 所以函数
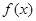 在区间
在区间 上为单调减函数. ……14分
上为单调减函数. ……14分点评:此题第一问求解析式时,不要忘记
 ,证明函数的单调性,只能用单调性的定义或导数(选修中将会学到).
,证明函数的单调性,只能用单调性的定义或导数(选修中将会学到).
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
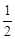 )=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(
)=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(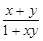 ),试证明:
),试证明: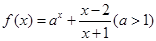 .
.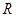 的函数
的函数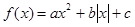
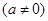 有四个单调区间,则实数
有四个单调区间,则实数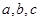 满足( )
满足( )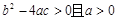
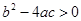
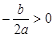
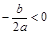
 是方程
是方程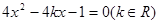 的两个不等实根,函数
的两个不等实根,函数 的定义域为
的定义域为 .
. 时,求函数
时,求函数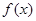 的值域;
的值域; ,
, 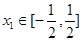 ,总存在
,总存在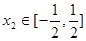 ,使得
,使得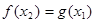 成立,
成立, 的取值范围.
的取值范围.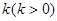 .现已知相距
.现已知相距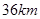 的
的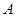 ,
,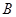 两家化工厂(污染源)的污染强度分别为正数
两家化工厂(污染源)的污染强度分别为正数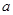 ,
,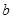 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数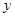 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设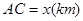 .
.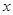 的函数;
的函数; 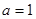 时,
时,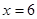 处取得最小值,试求
处取得最小值,试求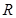 上的函数
上的函数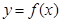 满足
满足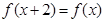 ,当
,当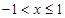 时,
时,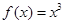 ,若函数
,若函数 至少有6个零点,则
至少有6个零点,则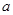 的取值范围是 ( )
的取值范围是 ( )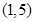
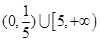
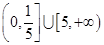
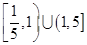
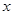 米,且宽减少
米,且宽减少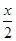 米时面积最大,此时宽减少了________米,面积取得了最大值。
米时面积最大,此时宽减少了________米,面积取得了最大值。