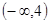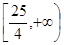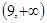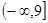题目内容
已知函数f(x)在(-1,1)上有定义,f(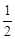 )=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(
)=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(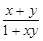 ),试证明:
),试证明:
(1)f(x)为奇函数;
(2)f(x)在(-1,1)上单调递减.
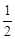 )=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(
)=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(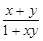 ),试证明:
),试证明:(1)f(x)为奇函数;
(2)f(x)在(-1,1)上单调递减.
见解析
【错解分析】本题知识依托:奇偶性及单调性定义及判定、赋值法及转化思想.对函数的奇偶性、单调性的判定以及运算能力和逻辑推理能力要求较高. 如果“赋值”不够准确,运算技能不过关,结果很难获得. 对于(1),获得f(0)的值进而取x=-y是解题关键;对于(2),判定
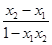 的范围是解题的焦点.
的范围是解题的焦点.【正解】(1)由f(x)+f(y)=f(
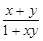 ),令x=y=0,得f(0)=0,
),令x=y=0,得f(0)=0,令y=-x,得f(x)+f(-x)=f(
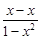 )=f(0)=0.
)=f(0)=0.∴f(x)=-f(-x).∴f(x)为奇函数.
(2)先证f(x)在(0,1)上单调递减.
令0<x1<x2<1,则f(x2)-f(x1)=f(x2)+f(-x1)=f(
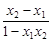 )
)∵0<x1<x2<1,∴x2-x1>0,1-x1x2>0,
∴
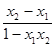 >0,又(x2-x1)-(1-x2x1)=(x2-1)(x1+1)<0
>0,又(x2-x1)-(1-x2x1)=(x2-1)(x1+1)<0∴x2-x1<1-x2x1,∴0<
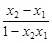 <1,
<1,由题意知f(
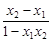 )<0,即f(x2)<f(x1).
)<0,即f(x2)<f(x1).∴f(x)在(0,1)上为减函数,又f(x)为奇函数且f(0)=0.
∴f(x)在(-1,1)上为减函数.
【点评】对于抽象函数函数性质的讨论、计算和证明,解题技巧、综合运用各类知识和技能的要求非常高;特别是最近几年,以一种“定义新函数”的题型出现,突出考核学生的学习能力、应用能力和创新能力,不特别强调解题的技巧。具体的差别,可以通过例题的练习和讲解来得以区分。总之,关于抽象函数题的难度都是相当高的

练习册系列答案
相关题目
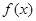 为定义在
为定义在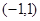 上的奇函数,当
上的奇函数,当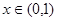 时,
时,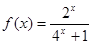 ;
;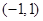 上的解析式;
上的解析式;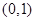 上的单调性,并给出证明.
上的单调性,并给出证明.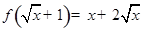 ,则
,则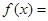 。(指出
。(指出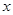 范围)
范围)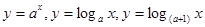 ,
,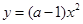 的图象,则与函数
的图象,则与函数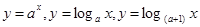 ,
,
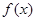 =
=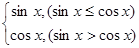 ,给出下列四个命题:①该函数是以
,给出下列四个命题:①该函数是以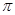 为最小正周期的周期函数;②当且仅当
为最小正周期的周期函数;②当且仅当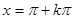 (k∈Z)时,该函数取得最小值-1;
(k∈Z)时,该函数取得最小值-1;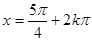 (k∈Z)对称;
(k∈Z)对称;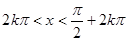 (k∈Z)时,0<
(k∈Z)时,0<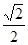 .
.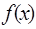 为奇函数,且在
为奇函数,且在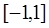 上为增函数,
上为增函数,  , 若
, 若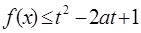 对所有
对所有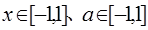 都成立,求
都成立,求 的取值范围。
的取值范围。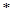 ”:
”: ,
, ,则函数
,则函数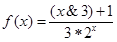
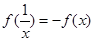 的函数,我们称为满足“倒负”变换的函数,下列函数:①
的函数,我们称为满足“倒负”变换的函数,下列函数:①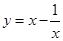 ;②
;②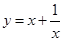 ;③
;③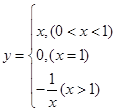 中满足“倒负”变换的函数是( )
中满足“倒负”变换的函数是( )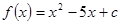 ,
,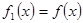 ,
,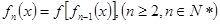 ,
,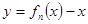 不存在零点,则
不存在零点,则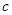 的范围是 ( )
的范围是 ( )