题目内容
(本小题满分16分)知函数f(x)=ax3+bx2+cx+d(a、b、c、d![]() R),且函数f(x)的图象关于原点对称,其图象x=3处的切线方程为8x-y-18=0.
R),且函数f(x)的图象关于原点对称,其图象x=3处的切线方程为8x-y-18=0.
(1)求f(x)的解析式;
(2)是否存在区间![]() ,使得函数f(x)的定义域和值域均为
,使得函数f(x)的定义域和值域均为![]() ?若存在,求出这样的一个区间
?若存在,求出这样的一个区间![]() ;若不存在,则说明理由;
;若不存在,则说明理由;
(3)若数列{an}满足:a1≥1,an+1≥![]() ,试比较+++…+与1的大小关系,并说明理由.
,试比较+++…+与1的大小关系,并说明理由.
(1)∵f(x)的图像关于原点对称,
∴f(-x)+f(x)=0恒成立, 即2bx2+2d≡0,∴b=d=0……………………2分
又f(x)的图像在x=3处的切线方程为8x-y-18=0,即 y-6=8(x-3),
∴f '(3)=8,且f(3)=6, 而f(x)=ax3+cx,∴f '(x)=3ax2+c
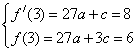 ……………………4分
……………………4分
解得 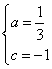 故所求的解析式为f(x)=x3-x ……………5分
故所求的解析式为f(x)=x3-x ……………5分
(2)解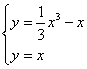 ,得x=0或x=± ……………………6分
,得x=0或x=± ……………………6分
又f '(x)=x2-1,由f '(x)=0得x=±1,
且当x∈[-,-1]或x∈[1,]时,f '(x)>0;
当x∈[-1,1]时 f '(x)< 0
∴f(x)在[-,-1]和[1,]上分别递增;在[—1,1]递减.
∴f(x)在[-,]上的极大值和极小值分别为f(-1)= ,f(1)=- ………8分
而-<-< <
故存在这样的区间![]() ,其中一个区间为[-,] ……………………10分
,其中一个区间为[-,] ……………………10分
(3)由(2)知f ' (x)=x2-1,∴an+1≥(an+1)2-1
而函数y=(x+1)2—1=x2+2x在[1,+∞)单调递增,
∴由al≥1,可知,a2≥(al+1)2—1=22—l;进而可得a3≥(a2+1)2—1≥23—1;…
由此猜想an≥2n—1. …………………12分
下面用数学归纳法证明:
①当n=1时,al≥1=21-1,结论成立
②假设n=k时有ak≥2k-1,
则当n=k+1时,
由f(x)=x2+2x在[1,+∞)上递增可知,
ak+1≥(ak+1)2-1≥(ak-1+1)2-1=2k+1-1,
即n=k+1时结论成立 …………………14分
∴对任意的n∈N+都有an≥2n—1,即1+an≥2n, ∴≤
∴+++…+≤+++…+
==1-()n<l
故 +++…+<l ……………………16分

 在平面直角坐标系
在平面直角坐标系 ,
, (
( ),
),
 ,对任意
,对任意 时,
时, 恒成立,求实数
恒成立,求实数 的范围;
的范围; ,当“
,当“ 在
在 的最大值.
的最大值. :方程
:方程 无实数根;
命题
无实数根;
命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.