题目内容
已知命题 :
: 在
在 上是增函数;命题
上是增函数;命题 函数
函数 存在极大值和极小值。求使命题“
存在极大值和极小值。求使命题“ 且
且 ”为真命题的
”为真命题的 的取值范围。
的取值范围。
[-3,1].
解析试题分析: 在
在 上是增函数,
上是增函数,
则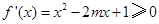 在
在 上恒成立, 3分
上恒成立, 3分 在
在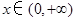 时上恒成立, 4分
时上恒成立, 4分
而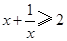 5分
5分
故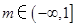 6分
6分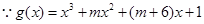 存在极大值与极小值,
存在极大值与极小值,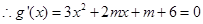 有两个不等的实根, 8分
有两个不等的实根, 8分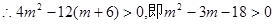 , 9分
, 9分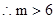 或
或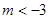 . 11分
. 11分
要使命题“p且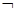 q”为真,则当且仅当p与
q”为真,则当且仅当p与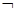 q均为真命题,
q均为真命题,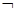 q为真命题时,
q为真命题时,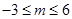 12分
12分
只需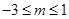 ,故m的取值范围为[-3,1]. 13分
,故m的取值范围为[-3,1]. 13分
考点:利用导数研究函数的单调性;利用导数研究函数的极值;复合命题真假的判断。
点评:此题虽说简单,但易错,出错的地方是:由“ 在
在 上是增函数”应得到“
上是增函数”应得到“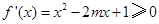 在
在 上恒成立且不恒为0”,而不是“
上恒成立且不恒为0”,而不是“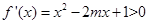 在
在 上恒成立”.我们一定要注意。
上恒成立”.我们一定要注意。

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 +2x0-m-1=0,且p∧q为真,求实数m的取值范围.
+2x0-m-1=0,且p∧q为真,求实数m的取值范围.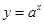 在R上单调递增,命题q:不等式
在R上单调递增,命题q:不等式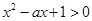 对于
对于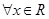 恒成立,若“
恒成立,若“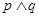 ”为假,“
”为假,“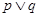 ”为真,求实数
”为真,求实数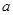 的取值范围
的取值范围 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线 的离心率
的离心率 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。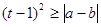 ,其中
,其中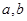 满足条件:五个数
满足条件:五个数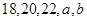 的平均数是20,标准差是
的平均数是20,标准差是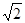 ; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆
; 命题q:m≤t≤n ,其中m,n满足条件:点M在椭圆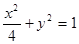 上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。
上,定点A(1,0),m、n分别为线段AM长的最小值和最大值。若命题“p或q”为真且命题“p且q”为假,求实数t的取值范围。 :实数
:实数 满足
满足 ,其中
,其中 ;命题
;命题 :实数
:实数
 ,且
,且 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.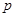 :方程
:方程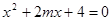 有实数根;命题
有实数根;命题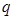 :方程
:方程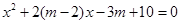 有实数根.已知
有实数根.已知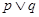 为真,
为真,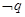 为真,求实数
为真,求实数 的取值范围.
的取值范围. :
: 是减函数,命题
是减函数,命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为 ,如果“
,如果“ 的取值范围.
的取值范围.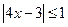 ,命题Q:
,命题Q: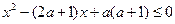 ,若
,若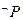 是
是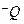 的必要不充分条件,求实数
的必要不充分条件,求实数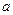 的取值范围
的取值范围