题目内容
(14分)设数列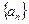 满足
满足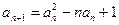 ,
,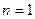 ,2,3…
,2,3…
(1)、当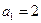 时
时 ,求
,求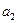 ,
,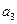 ,
,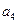 ,并由此猜想出
,并由此猜想出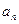 的
的 一个通项公式。
一个通项公式。
(2)、当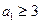 时,证明对所有的
时,证明对所有的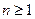 ,有
,有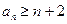 。
。
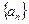 满足
满足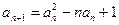 ,
,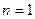 ,2,3…
,2,3…(1)、当
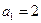 时
时 ,求
,求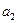 ,
,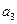 ,
,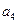 ,并由此猜想出
,并由此猜想出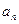 的
的 一个通项公式。
一个通项公式。(2)、当
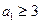 时,证明对所有的
时,证明对所有的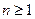 ,有
,有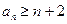 。
。(1)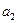 ="3,"
="3," 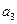 =4,
=4,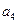 =5,猜想
=5,猜想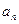 =n﹢1(n≧1)。
=n﹢1(n≧1)。
(2)略
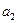 ="3,"
="3," 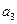 =4,
=4,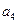 =5,猜想
=5,猜想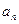 =n﹢1(n≧1)。
=n﹢1(n≧1)。(2)略
略

练习册系列答案
相关题目
题目内容
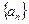 满足
满足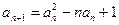 ,
,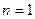 ,2,3…
,2,3…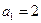 时
时 ,求
,求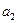 ,
,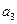 ,
,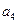 ,并由此猜想出
,并由此猜想出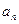 的
的 一个通项公式。
一个通项公式。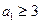 时,证明对所有的
时,证明对所有的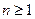 ,有
,有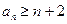 。
。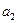 ="3,"
="3," 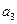 =4,
=4,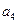 =5,猜想
=5,猜想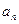 =n﹢1(n≧1)。
=n﹢1(n≧1)。