题目内容
正方体ABCD-A1B1C1D1的棱长为2,MN是它的内切球的一条弦(我们把球面上任意两点之间的线段称为球的弦),P为正方体表面上的动点,当弦MN的长度最大时,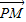 •
•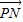 的取值范围是 .
的取值范围是 .
【答案】分析:根据题意,可设M、N分别是内切球在正方体左、右侧面的切点,运动点P并加以观察,可得当P与正方体的某个顶点重合时,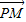 •
•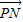 达到最大值;当P与正方体某个面的中心重合时,
达到最大值;当P与正方体某个面的中心重合时,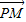 •
•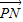 达到最小值.由此结合数量积的计算公式,即可得到数量积
达到最小值.由此结合数量积的计算公式,即可得到数量积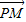 •
•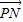 的取值范围.
的取值范围.
解答: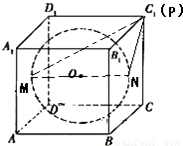 解:根据题意,MN是正方体内切球的最大弦长
解:根据题意,MN是正方体内切球的最大弦长
∴MN是内切球的直径
设M、N分别是内切球在正方体左、右侧面的切点,如图
当P在正方体表面运动,它与正方体的某个顶点重合时,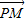 •
•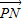 达到最大值.
达到最大值.
以C1点为例,此时
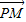 •
•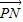 =
=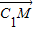 •
•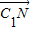 =
=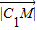 •
•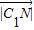 cos∠∠MC1N=
cos∠∠MC1N=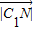 2=(
2=(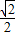
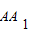 )2=2;
)2=2;
当点P与正方体某个面的中心重合时,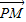 •
•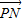 达到最小值.
达到最小值.
此时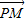 ⊥
⊥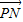 ,得
,得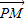 •
•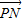 =0
=0
综上所述,得数量积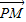 •
•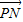 的取值范围为[0,2]
的取值范围为[0,2]
故答案为:[0,2]
点评:本题给出正方体的内切球,求一个数量积的取值范围.着重考查了平面向量数量积的运算和正方体的性质等知识,属于基础题.
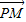 •
•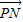 达到最大值;当P与正方体某个面的中心重合时,
达到最大值;当P与正方体某个面的中心重合时,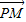 •
•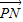 达到最小值.由此结合数量积的计算公式,即可得到数量积
达到最小值.由此结合数量积的计算公式,即可得到数量积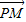 •
•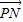 的取值范围.
的取值范围.解答:
 解:根据题意,MN是正方体内切球的最大弦长
解:根据题意,MN是正方体内切球的最大弦长∴MN是内切球的直径
设M、N分别是内切球在正方体左、右侧面的切点,如图
当P在正方体表面运动,它与正方体的某个顶点重合时,
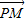 •
•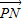 达到最大值.
达到最大值.以C1点为例,此时
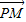 •
•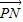 =
=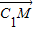 •
•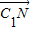 =
=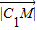 •
•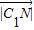 cos∠∠MC1N=
cos∠∠MC1N=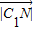 2=(
2=(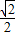
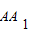 )2=2;
)2=2;当点P与正方体某个面的中心重合时,
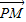 •
•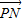 达到最小值.
达到最小值.此时
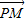 ⊥
⊥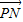 ,得
,得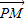 •
•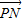 =0
=0综上所述,得数量积
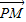 •
•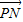 的取值范围为[0,2]
的取值范围为[0,2]故答案为:[0,2]
点评:本题给出正方体的内切球,求一个数量积的取值范围.着重考查了平面向量数量积的运算和正方体的性质等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: 已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点.
已知边长为6的正方体ABCD-A1B1C1D1,E,F为AD、CD上靠近D的三等分点,H为BB1上靠近B的三等分点,G是EF的中点. 如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积.
如图所示,在棱长为2cm的正方体ABCD-A1B1C1D1中,A1B1的中点是P,过点A1作出与截面PBC1平行的截面,简单证明截面形状,并求该截面的面积. 如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )
如图,正方体ABCD-A1B1C1D1中,M是棱AB的中点,过A1,M,C三点的平面与CD所成角正弦值( )