题目内容
已知m=(2cos x+2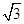 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调递增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f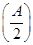 =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.
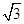 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.(1)将y表示为x的函数f(x),并求f(x)的单调递增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f
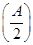 =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.(1)单调递增区间为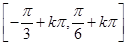 ,k∈Z(2)
,k∈Z(2)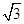
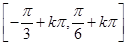 ,k∈Z(2)
,k∈Z(2)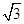
(1)由m⊥n得m·n=0,2cos2x+2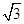 sin xcos x-y=0,
sin xcos x-y=0,
即y=2cos2x+2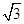 sin xcos x=cos 2x+
sin xcos x=cos 2x+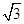 sin 2x+1=2sin
sin 2x+1=2sin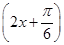 +1.
+1.
令-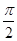 +2kπ≤2x+
+2kπ≤2x+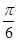 ≤
≤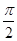 +2kπ,k∈Z,
+2kπ,k∈Z,
则-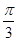 +kπ≤x≤
+kπ≤x≤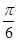 +kπ,k∈Z,
+kπ,k∈Z,
故f(x)的单调递增区间为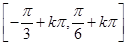 ,k∈Z.
,k∈Z.
(2)因为f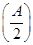 =3,所以2sin
=3,所以2sin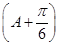 +1=3,sin
+1=3,sin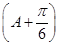 =1,
=1,
所以A+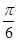 =2kπ+
=2kπ+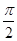 ,k∈Z.因为0<A<π,所以A=
,k∈Z.因为0<A<π,所以A=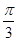 .
.
由余弦定理得:a2=b2+c2-2bccos A,即4=b2+c2-bc,
所以4=(b+c)2-3bc,
因为b+c=4,所以bc=4.所以S△ABC=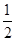 bcsin A=
bcsin A=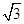 .
.
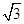 sin xcos x-y=0,
sin xcos x-y=0,即y=2cos2x+2
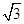 sin xcos x=cos 2x+
sin xcos x=cos 2x+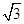 sin 2x+1=2sin
sin 2x+1=2sin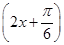 +1.
+1.令-
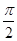 +2kπ≤2x+
+2kπ≤2x+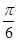 ≤
≤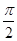 +2kπ,k∈Z,
+2kπ,k∈Z,则-
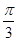 +kπ≤x≤
+kπ≤x≤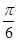 +kπ,k∈Z,
+kπ,k∈Z,故f(x)的单调递增区间为
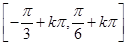 ,k∈Z.
,k∈Z.(2)因为f
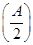 =3,所以2sin
=3,所以2sin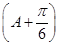 +1=3,sin
+1=3,sin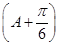 =1,
=1,所以A+
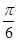 =2kπ+
=2kπ+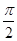 ,k∈Z.因为0<A<π,所以A=
,k∈Z.因为0<A<π,所以A=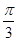 .
.由余弦定理得:a2=b2+c2-2bccos A,即4=b2+c2-bc,
所以4=(b+c)2-3bc,
因为b+c=4,所以bc=4.所以S△ABC=
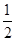 bcsin A=
bcsin A=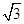 .
.
练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
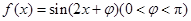 的图像经过点
的图像经过点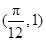 .
. 的值;
的值; 中,
中,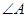 、
、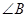 、
、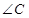 所对的边分别为
所对的边分别为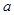 、
、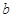 、
、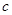 ,若
,若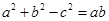 ,且
,且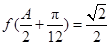 .求
.求 .
.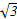 ),且m⊥n.
),且m⊥n.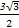 ,a=2,求b的值.
,a=2,求b的值. 经过圆心
经过圆心 ,
, ,
, 绕点
绕点 转到
转到 ,连
,连 交圆
交圆 ,则
,则 ______________________
______________________
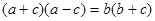 ,则
,则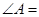 ( )
( )



 ,b=1,c=2,则A=________.
,b=1,c=2,则A=________.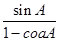 = .
= .