题目内容
下列命题正确的个数（1）很小的实数可以构成集合；
（2）集合{y|y=x2-1}与集合{（x，y）|y=x2-1}是同一个集合；
（3）1，
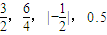，这些数组成的集合有5个元素；（4）集合{（x，y）|xy≤0，x，y∈R}是指第二和第四象限内的点集．
【答案】分析：利用集合的元素的特点：确定性、互异性、无序性判断出（1）（3）错；利用集合的表示法中的描述法要看代表元素判断出（2）错；利用象限中点坐标的特点判断出（4）错．
解答：解：对于（1）“很小”不确定，故（1）错
对于（2）集合{y|y=x2-1}表示的是函数y=x2-1的值域；
而集合{（x，y）|y=x2-1}表示的是y=x2-1图象上的点，故（2）错
对于（3）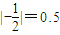
；
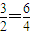，所以
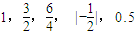些数组成的集合有3个元素，故（3）错
对于（4））集合{（x，y）|xy≤0，x，y∈R}是指第二和第四象限内的点集及两个坐标轴上的点，故（4）错
故答案为：0
点评：本题考查集合的 元素的三要素：确定性、互异性、无序性；集合的表示法：描述法．
解答：解：对于（1）“很小”不确定，故（1）错
对于（2）集合{y|y=x2-1}表示的是函数y=x2-1的值域；
而集合{（x，y）|y=x2-1}表示的是y=x2-1图象上的点，故（2）错
对于（3）
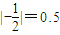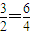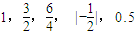；，所以些数组成的集合有3个元素，故（3）错对于（4））集合{（x，y）|xy≤0，x，y∈R}是指第二和第四象限内的点集及两个坐标轴上的点，故（4）错
故答案为：0
点评：本题考查集合的 元素的三要素：确定性、互异性、无序性；集合的表示法：描述法．
练习册系列答案
一本好题口算题卡系列答案
相关题目