题目内容
下列命题正确的个数为( )
①斜线与它在平面内的射影所成的角是这条斜线和这个平面内所有直线所成的角的最小角.
②二面角α-l-β的平面角是过棱l上任一点O,分别在两个半平面内任意两条射线OA,OB所成角的∠AOB的最大角.
③如果一条直线和一个平面的一条斜线垂直,那么它也和这条斜线在这个平面内的射影垂直.
④设A是空间一点,
为空间任一非零向量,适合条件的集合{
|
•
=0}的所有点M构成的图形是过点A且与
垂直的一个平面.
①斜线与它在平面内的射影所成的角是这条斜线和这个平面内所有直线所成的角的最小角.
②二面角α-l-β的平面角是过棱l上任一点O,分别在两个半平面内任意两条射线OA,OB所成角的∠AOB的最大角.
③如果一条直线和一个平面的一条斜线垂直,那么它也和这条斜线在这个平面内的射影垂直.
④设A是空间一点,
| n |
| M |
| AM |
| n |
| n |
分析:①根据面角的定义可以判断正确.②利用二面角的定义判断.③根据线面垂直的性质判断正确.④根据空间向量垂直的定义和性质可以判断.
解答:解:①根据斜线和平面所成角的定义和性质可知斜线与它在平面内的射影所成的角是这条斜线和这个平面内所有直线所成的角的最小角,所以正确.
②根据二面角平面角的定义可知,二面角的平面角和∠AOB的大小不确定,所以错误.
③根据线面垂直的判定定理和性质可知要使结论成立,必须要求该直线在平面内,否则不成立,所以错误.
④由{
|
•
=0},向量
和
垂直h或
=0,所以适合条件的集合{
|
•
=0}的所有点M构成的图形是过点A且与
垂直的一个平面,所以正确.
故选B.
②根据二面角平面角的定义可知,二面角的平面角和∠AOB的大小不确定,所以错误.
③根据线面垂直的判定定理和性质可知要使结论成立,必须要求该直线在平面内,否则不成立,所以错误.
④由{
| M |
| AM |
| n |
| AM |
| n |
| AM |
| M |
| AM |
| n |
| n |
故选B.
点评:本题主要考查和空间几何有关的命题的真假判断,考查学生对概念的理解和把握.综合性较强.

练习册系列答案
相关题目
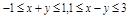 ,则
,则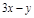 的范围是
的范围是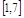 ;
;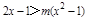 对满足
对满足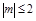 的所有m都成立,则x的范围是
的所有m都成立,则x的范围是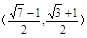 ;
;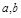 满足
满足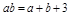 ,则
,则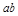 的取值范围是
的取值范围是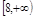
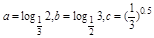 大小关系是
大小关系是