题目内容
若数列{an}满足an+2+pan+1+qan=0(其中p2+q2≠0,且p、q为常数)对任意n∈N*都成立,则我们把数列{an}称为“L型数列”.(1)试问等差数列{an}、等比数列{bn}(公比为r)是否为L型数列?若是,写出对应p、q的值;若不是,说明理由.
(2)已知L型数列{an}满足a1=1,a2=3,an+1-4an+4an-1=0(n≥2,n∈N*),证明:数列{an+1-2an}是等比数列,并进一步求出{an}的通项公式an.
【答案】分析:(1)等差数列{an}、等比数列{bn}(n∈N*)都是L型数列,然后分别找出符合题意的p和q即可.
(2)将an+1-4an+4an-1=0(n≥2,n∈N*)化成an+1-2an=2an-4an-1=2(an-2an-1),根据等比数列的定义进行判定即可,然后求出新数列的通项,在等式两侧同除以2n,可得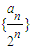 是以
是以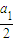 为首项,公差为
为首项,公差为 的等差数列,求出通项即可求出an.
的等差数列,求出通项即可求出an.
解答:解:(1)答:等差数列{an}、等比数列{bn}(n∈N*)都是L型数列.
理由 当数列{an}(n∈N*)是等差数列时,有an+2-an+1=an+1-an,(1分)
即an+2-2an+1+an=0,且相应的p=-2,q=1. (3分)
所以等差数列{an}(n∈N*)是L型数列. (4分)
同样,当数列{bn}(n∈N*)是等比数列时,有bn+2=rbn+1(r为公比),(5分)
即bn+2-rbn+1+0•bn=0,且相应的p=-r,q=0. (7分)
所以等比数列{bn}(n∈N*)是L型数列. (8分)
证明 (2)∵an+1-4an+4an-1=0(n≥2,n∈N*),
∴an+1-2an=2an-4an-1
=2(an-2an-1). (10分)
又a2-2a1=3-2=1(≠0),
∴数列{an+1-2an}(n∈N*)是以(a2-2a1)为首项,公比为2的等比数列. (12分)
于是,an-2an-1=(a2-2a1)•2n-2,即an-2an-1=2n-2(n≥2,n∈N*).
∴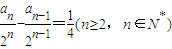 .因此,
.因此,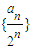 是以
是以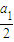 为首项,公差为
为首项,公差为 的等差数列.(14分)
的等差数列.(14分)
∴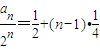 ,
,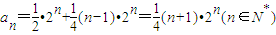
所以数列{an}的通项公式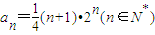 . (16分)
. (16分)
点评:本题主要考查了等差数列与等比数列的综合,同时考查了数列的通项公式,构造新数列是常用的方法,属于中档题.
(2)将an+1-4an+4an-1=0(n≥2,n∈N*)化成an+1-2an=2an-4an-1=2(an-2an-1),根据等比数列的定义进行判定即可,然后求出新数列的通项,在等式两侧同除以2n,可得
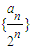 是以
是以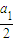 为首项,公差为
为首项,公差为 的等差数列,求出通项即可求出an.
的等差数列,求出通项即可求出an.解答:解:(1)答:等差数列{an}、等比数列{bn}(n∈N*)都是L型数列.
理由 当数列{an}(n∈N*)是等差数列时,有an+2-an+1=an+1-an,(1分)
即an+2-2an+1+an=0,且相应的p=-2,q=1. (3分)
所以等差数列{an}(n∈N*)是L型数列. (4分)
同样,当数列{bn}(n∈N*)是等比数列时,有bn+2=rbn+1(r为公比),(5分)
即bn+2-rbn+1+0•bn=0,且相应的p=-r,q=0. (7分)
所以等比数列{bn}(n∈N*)是L型数列. (8分)
证明 (2)∵an+1-4an+4an-1=0(n≥2,n∈N*),
∴an+1-2an=2an-4an-1
=2(an-2an-1). (10分)
又a2-2a1=3-2=1(≠0),
∴数列{an+1-2an}(n∈N*)是以(a2-2a1)为首项,公比为2的等比数列. (12分)
于是,an-2an-1=(a2-2a1)•2n-2,即an-2an-1=2n-2(n≥2,n∈N*).
∴
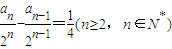 .因此,
.因此,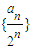 是以
是以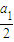 为首项,公差为
为首项,公差为 的等差数列.(14分)
的等差数列.(14分)∴
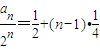 ,
,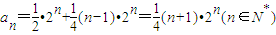
所以数列{an}的通项公式
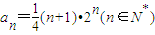 . (16分)
. (16分)点评:本题主要考查了等差数列与等比数列的综合,同时考查了数列的通项公式,构造新数列是常用的方法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )

 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )
