题目内容
下列关于数列的命题中,正确的是( )
分析:由等差数列的通项公式验证选项A,由等比中项的概念求解-2和-8的等比中项验证选项C,利用举特例的办法排除选项B和D.
解答:解:若数列{an}是等差数列,设其首项为a1,公差为d,
由p+q=r(p,q,r∈N*),
则ap+aq=a1+(p-1)d+a1+(q-1)d=2a1+(p+q-2)d
=2a1+(r-2)d=2[a1+(
-1)d]=2a
,
∴选项A不正确;
数列0,0,0,0,…满足an+1=2an,该数列不是等比数列,
∴选项B不正确;
设-2和-8的等比中项为m,则m=±
=±4,
∴选项C正确;
当等差数列的公差为0时,其通项公式为an=f(n)=a1,不是关于n的一次函数,
∴选项D不正确.
故选:C.
由p+q=r(p,q,r∈N*),
则ap+aq=a1+(p-1)d+a1+(q-1)d=2a1+(p+q-2)d
=2a1+(r-2)d=2[a1+(
| r |
| 2 |
| r |
| 2 |
∴选项A不正确;
数列0,0,0,0,…满足an+1=2an,该数列不是等比数列,
∴选项B不正确;
设-2和-8的等比中项为m,则m=±
| (-2)×(-8) |
∴选项C正确;
当等差数列的公差为0时,其通项公式为an=f(n)=a1,不是关于n的一次函数,
∴选项D不正确.
故选:C.
点评:本题考查了等差数列和等比数列的性质,考查了特殊化思想在解题中的应用,是基础题.

练习册系列答案
相关题目
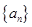 是等差数列,且
是等差数列,且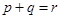 (
(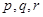 为正整数)则
为正整数)则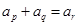
 是公比为2的等比数列
是公比为2的等比数列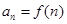 ,则
,则 是关于
是关于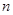 的一次函数
的一次函数