题目内容
若数列{an}满足a≤an≤b,其中a、b是常数,则称数列{an}为有界数列,a是数列{an}的下界,b是数列{an}的上界.现要在区间[-1,2)中取出20个数构成有界数列{bn},并使数列{bn}有且仅有两项差的绝对值小于 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )A.5
B.

C.7
D.

【答案】分析:因为m要最小,所以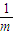 要最大,将区间[-1,2)等分成19个区间,每个的长度为
要最大,将区间[-1,2)等分成19个区间,每个的长度为 ,使数列{bn}有且仅有b19,b20两项差的绝对值小于
,使数列{bn}有且仅有b19,b20两项差的绝对值小于 ,则
,则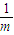 的最大值为
的最大值为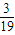 ,故m的最小值为
,故m的最小值为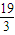 .
.
解答:解:因为m要最小,所以 要最大,
要最大,
将区间[-1,2)等分成19个区间,
每个的长度为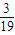 ,
,
b1,b2,…,b19取各段的左端点,
b20在第十九段上任取一点,
则使数列{bn}有且仅有b19,b20两项差的绝对值小于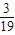 ,
,
则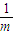 的最大值为
的最大值为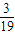 ,
,
∴m的最小值为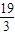 .
.
故选B.
点评:本题考查数列与函数的综合,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.
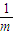 要最大,将区间[-1,2)等分成19个区间,每个的长度为
要最大,将区间[-1,2)等分成19个区间,每个的长度为 ,使数列{bn}有且仅有b19,b20两项差的绝对值小于
,使数列{bn}有且仅有b19,b20两项差的绝对值小于 ,则
,则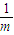 的最大值为
的最大值为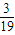 ,故m的最小值为
,故m的最小值为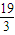 .
.解答:解:因为m要最小,所以
 要最大,
要最大,将区间[-1,2)等分成19个区间,
每个的长度为
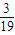 ,
,b1,b2,…,b19取各段的左端点,
b20在第十九段上任取一点,
则使数列{bn}有且仅有b19,b20两项差的绝对值小于
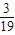 ,
,则
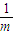 的最大值为
的最大值为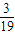 ,
,∴m的最小值为
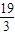 .
.故选B.
点评:本题考查数列与函数的综合,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 ,那么正数m的最小取值是( )
,那么正数m的最小取值是( )
