题目内容
13.若全集U={n|n是小于9的正整数},集合A={n∈U|n是奇数},B={n∈U|n是3的倍数},求:(1)A∩B
(2)∁U(A∪B)
分析 先求出满足条件的全集U,进而求出满足条件的集合A与集合B,结合集合的交集,并集,补集运算的定义,可得答案.
解答 解:∵U={n|n是小于9的正整数},
∴U={1,2,3,4,5,6,7,8},
则A={1,3,5,7},B={3,6},
∴(1)A∩B={3},
(2)A∪B={1,3,5,6,7},
∁U(A∪B)={2,4,8}
点评 本题考查的知识点是并集运算和补集运算,运算的关键是准确列举出满足条件的集合.

练习册系列答案
相关题目
3.不等式组$\left\{\begin{array}{l}{{x}^{2}-1<0}\\{{x}^{2}-3x>0}\end{array}\right.$的解集是( )
| A. | {x|-1<x<1} | B. | {x|-1<x<0} | C. | {x|0<x<1} | D. | {x|0<x<3} |
4.平面内到两定点F1、F2的距离之比等于常数m(m>0且m≠1)的点的轨迹称为阿波罗尼斯圆,已知曲线C是平面内到两定点F1(-1,0),F2(1,0)距离之比等于常数m(m>0,m≠1)的点的轨迹,下面选项正确的是( )
| A. | 曲线C关于坐标原点对称 | B. | 曲线C关于y轴对称 | ||
| C. | 曲线C关于x轴对称 | D. | 曲线C过坐标原点 |
1.点A位于双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上,F1F2是它的两个焦点,求△AF1F2的重心G的轨迹方程.
5.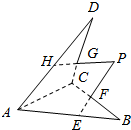 已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点,且直线EF交直线HG于点P,则点P的位置是必处在( )的上面.
已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点,且直线EF交直线HG于点P,则点P的位置是必处在( )的上面.
 已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点,且直线EF交直线HG于点P,则点P的位置是必处在( )的上面.
已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点,且直线EF交直线HG于点P,则点P的位置是必处在( )的上面.| A. | BD | B. | AD | C. | AC | D. | 平面BCD之内 |
2.若复数Z=$\frac{a+3i}{1-2i}$(a∈R,i是虚数单位)是纯虚数,则在复平面内Z对应点的坐标为( )
| A. | (0,2) | B. | (0,3i ) | C. | (0,3) | D. | (0,2i) |
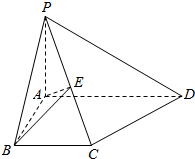 在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=1,AD=2,PA⊥底面ABCD,PD与底面成30°角.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=1,AD=2,PA⊥底面ABCD,PD与底面成30°角.