题目内容
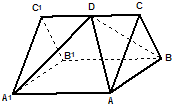 (2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点.
(2013•松江区二模)如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2,D为侧棱CC1的中点.(1)求异面直线A1D与BC所成角的大小(结果用反三角函数值表示);
(2)求直线A1B1到平面DAB的距离.
分析:(1)可通过建立空间直角坐标系,利用向量坐标运算求向量的夹角来求异面直线所成的角;或通过作平行线,再解三角形求解;
(2)根据转化思想,线面距离转化为点到平面的距离,再利用三棱锥的换底性求解.
(2)根据转化思想,线面距离转化为点到平面的距离,再利用三棱锥的换底性求解.
解答: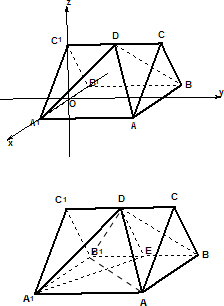 解:(1)方法一:
解:(1)方法一:
以A1B1中点O为坐标原点,如图建立空间直角坐标系.
由题意得A1(1,0,0),D(0,1,
),B(-1,2,0),C(0,2,
)
则
=(-1,1,
),
=(1,0,
)
设θ为向量
与
的夹角,cosθ=
=
,
∴异面直线A1D与BC所成角的大小为arccos
.
方法二:取B1B中点E,连结A1E,DE.∵DE∥CB
∴∠A1DE为异面直线A1D与BC所成的角.
在Rt△A1B1E中,A1E=
;在Rt△A1C1D中,A1D=
;
cos∠A1DE=
=
.
∴异面直线A1D与BC所成角的大小为arccos
.
(2)∵AB∥A1B1,∴A1B1∥平面ABD,
∴A1B1到平面DAB的距离即为A1到平面DAB的距离,设为h.
由题意得A1D=AD=BD=
,AB=2,
等腰△ADB底边AB上的高为
=2,S△ABD=
•2•2=2,则S△AA1B=2,
且D到平面ABB1A1的距离为
,
由VA1-ABD=VD-A1AB得
×S△ABD•h=
×S△A1AB×
,
∴h=
,
∴直线A1B1到平面DAB的距离为
.
 解:(1)方法一:
解:(1)方法一:以A1B1中点O为坐标原点,如图建立空间直角坐标系.
由题意得A1(1,0,0),D(0,1,
| 3 |
| 3 |
则
| A1D |
| 3 |
| BC |
| 3 |
设θ为向量
| A1D |
| BC |
| -1+3 | ||||||||
|
| ||
| 5 |
∴异面直线A1D与BC所成角的大小为arccos
| ||
| 5 |
方法二:取B1B中点E,连结A1E,DE.∵DE∥CB
∴∠A1DE为异面直线A1D与BC所成的角.
在Rt△A1B1E中,A1E=
| 5 |
| 5 |
cos∠A1DE=
| ||
| A1D |
| ||
| 5 |
∴异面直线A1D与BC所成角的大小为arccos
| ||
| 5 |
(2)∵AB∥A1B1,∴A1B1∥平面ABD,
∴A1B1到平面DAB的距离即为A1到平面DAB的距离,设为h.
由题意得A1D=AD=BD=
| 5 |
等腰△ADB底边AB上的高为
| 5-1 |
| 1 |
| 2 |
且D到平面ABB1A1的距离为
| 3 |
由VA1-ABD=VD-A1AB得
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
∴h=
| 3 |
∴直线A1B1到平面DAB的距离为
| 3 |
点评:本题考查异面直线所成的角及线面距离问题.

练习册系列答案
相关题目