题目内容
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,PD垂直底面ABCD,PD=2 R,E,F分别是PB,CD上的点,且
R,E,F分别是PB,CD上的点,且 ,过点E作BC的平行线交PC于G,
,过点E作BC的平行线交PC于G,
(1)求BD与平面ABP所成角θ的正弦值;
(2)证明:△EFG是直角三角形;
(3)当 时,求△EFG的面积.
时,求△EFG的面积.
 R,E,F分别是PB,CD上的点,且
R,E,F分别是PB,CD上的点,且 ,过点E作BC的平行线交PC于G,
,过点E作BC的平行线交PC于G,(1)求BD与平面ABP所成角θ的正弦值;
(2)证明:△EFG是直角三角形;
(3)当
 时,求△EFG的面积.
时,求△EFG的面积. 
解:(1)在Rt△BAD中,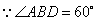 ,
,
∴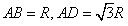 ,
,
而PD垂直底面ABCD,
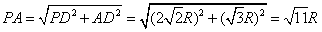 ,
,
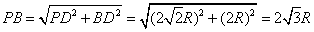 ,
,
在△PAB中,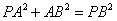 ,
,
即△PAB为以∠PAB为直角的直角三角形,
设点D到面PAB的距离为H,
由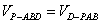 ,有
,有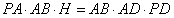 ,
,
即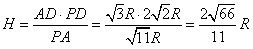 ,
,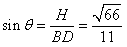 ;
;
(2) ,∴
,∴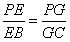 ,
,
而 ,即
,即 ,
,
∴ ,∴GF⊥BC,∴GF⊥EG,
,∴GF⊥BC,∴GF⊥EG,
∴△EFG是直角三角形;
(3) 时,
时, ,
,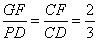 ,
,
即 ,
,
∴△EFG的面积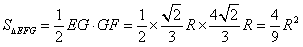 。
。
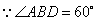 ,
,∴
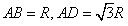 ,
,而PD垂直底面ABCD,
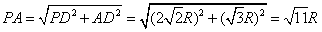 ,
,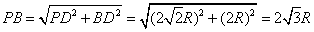 ,
,在△PAB中,
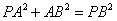 ,
,即△PAB为以∠PAB为直角的直角三角形,
设点D到面PAB的距离为H,
由
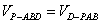 ,有
,有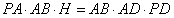 ,
,即
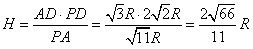 ,
,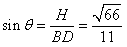 ;
;(2)
 ,∴
,∴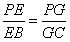 ,
,而
 ,即
,即 ,
,∴
 ,∴GF⊥BC,∴GF⊥EG,
,∴GF⊥BC,∴GF⊥EG,∴△EFG是直角三角形;
(3)
 时,
时, ,
,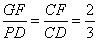 ,
,即
 ,
,∴△EFG的面积
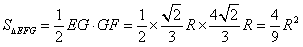 。
。 
练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.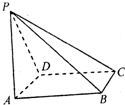 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,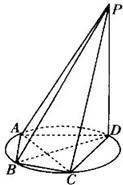 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.