题目内容
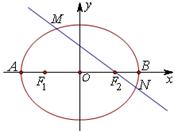 ()(本小题满分14分)已知中心在原点、焦点在x轴的椭圆的离心率为
()(本小题满分14分)已知中心在原点、焦点在x轴的椭圆的离心率为![]() ,且过点(
,且过点(![]() ,
,![]() ). (Ⅰ)求椭圆E的方程;(Ⅱ)若A,B是椭圆E的左、右顶点,直线
). (Ⅰ)求椭圆E的方程;(Ⅱ)若A,B是椭圆E的左、右顶点,直线![]() :
:![]() (
(![]() )与椭圆E交于
)与椭圆E交于![]() 、
、![]() 两点,证明直线
两点,证明直线![]() 与直线
与直线![]() 的交点在垂直于
的交点在垂直于![]() 轴的定直线上,并求出该直线方程.
轴的定直线上,并求出该直线方程.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
解析:
(Ⅰ)依题意,设椭圆![]() 的方程为
的方程为![]() ,
,
由已知![]() =
=![]() . ① ∵点(
. ① ∵点(![]() ,
,![]() )在椭圆E上,∴
)在椭圆E上,∴![]() +
+![]() =1. ②
=1. ②
由①、②及![]() 解得,
解得,![]() ,
,![]() .∴椭圆
.∴椭圆![]() 的方程为
的方程为![]() .…6分
.…6分
(Ⅱ)将直线![]() :
:![]() ,代入椭圆方程
,代入椭圆方程![]() 并整理,得
并整理,得![]() , 设直线
, 设直线![]() 与椭圆
与椭圆![]() 的交点
的交点![]() ,
,![]() ,
,
由根与系数的关系,得![]() ,
,![]() . ……9分
. ……9分
消去![]() 得,
得,![]() . 直线
. 直线![]() 的方程为:
的方程为:![]() ,
,
即![]() .直线
.直线![]() 的方程为:
的方程为:![]() ,
,
即![]() .12分由直线
.12分由直线![]() 与直线
与直线![]() 的方程消去
的方程消去![]() 得,
得,
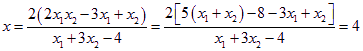 .
.
∴直线![]() 与直线
与直线![]() 的交点在定直线
的交点在定直线![]() 上. …14分
上. …14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)