题目内容
16．已知定义域在R上的函数，具有下列三个性质：①在（-∞，-1）上单调减函数；②函数具有奇偶性；③函数有最小值为0．
满足上述三个条件的函数可以是f（x）=x2．
分析 根据基本初等函数、函数的性质和题意，选择一个最简单的二次函数即可．
解答 解：∵f（x）=x2在（-∞，0）上是减函数，
满足①在（-∞，-1）上单调减函数；
且是偶函数，
满足②函数具有奇偶性；
在定义域上的最小值是0，
满足③函数有最小值为0．
∴函数可以是f（x）=x2，
故答案为：f（x）=x2（答案不唯一）
点评 本题是一个开放型的题目，主要考查了函数的基本性质和对初等函数的掌握情况．
练习册系列答案
相关题目
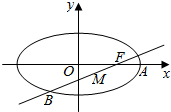椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）斜率为$\frac{b}{a}$的直线与椭圆C交于A、B两点（如图），AB中点为M，MA中点时椭圆C的右焦点F，求椭圆C的离心率e．