题目内容
过抛物线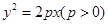 的焦点F作直线交抛物线于A、 B两点,O为抛物线的顶点。则△ABO是一个
的焦点F作直线交抛物线于A、 B两点,O为抛物线的顶点。则△ABO是一个
A.等边三角形; B.直角三角形;
C.不等边锐角三角形; D.钝角三角形
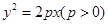 的焦点F作直线交抛物线于A、 B两点,O为抛物线的顶点。则△ABO是一个
的焦点F作直线交抛物线于A、 B两点,O为抛物线的顶点。则△ABO是一个A.等边三角形; B.直角三角形;
C.不等边锐角三角形; D.钝角三角形
D
分析:设出A,B点坐标,以及直线AB的方程,联立直线方程与抛物线方程,用向量的坐标公式求,再代入向量的夹角公式,求出∠AOB的余弦值,再判断正负即可。
解答:
设A(x1,y1),B(x2,y2),AB方程x="my+" p/2,
由 x=my+p/2;y2=2px;
得y2-2pmy-p2=0,∴y1y2=-p2,x1x2= p2/4
∴x1x2+y1y2=-p2+ p2/4=-3/4p2<0
∴cos∠AOB<0,
∴∠AOB为钝角,△ABO为钝角三角形,故选D。
点评:本题考查了直线与抛物线的位置关系,关键是用坐标表示向量的数量积。

练习册系列答案
相关题目

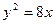 ,焦点为F,有一定点
,焦点为F,有一定点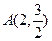 ,A在抛物线准线上的射影为H,P为抛物线上一动点.
,A在抛物线准线上的射影为H,P为抛物线上一动点.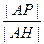 ;
;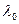 是过点A且垂直于x轴的直线,是否存在直线
是过点A且垂直于x轴的直线,是否存在直线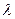 ,使得
,使得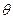 的范围;若不存在,请
的范围;若不存在,请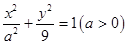 与双曲线
与双曲线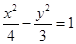 有相同的焦点, 则
有相同的焦点, 则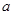 的值为( )
的值为( )
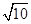
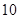
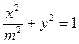 (常数
(常数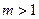 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右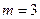 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.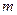 的取值范围.
的取值范围.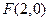 的抛物线的标准方程是
的抛物线的标准方程是 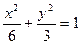 ,则其离心率为
,则其离心率为 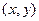 满足
满足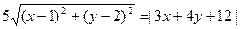 ,则M点的轨迹曲线为 .
,则M点的轨迹曲线为 .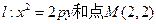 ,若抛物线
,若抛物线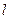 上存在不同两点A、B满足
上存在不同两点A、B满足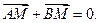
 值范围;
值范围; 存在,求出点C的坐标;若不存在,请说明理由。
存在,求出点C的坐标;若不存在,请说明理由。