题目内容
数列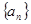 的通项为
的通项为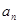 =
=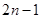 ,
, ,其前
,其前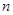 项和为
项和为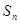 ,则使
,则使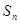 >48成立的
>48成立的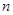 的最小值为( )
的最小值为( )
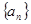 的通项为
的通项为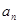 =
=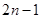 ,
, ,其前
,其前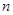 项和为
项和为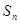 ,则使
,则使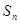 >48成立的
>48成立的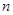 的最小值为( )
的最小值为( )| A.7 | B.8 | C.9 | D.10 |
A
分析:由an=2n-1可得数列{an}为等差数列,然后根据等差数列的求和公式求出Sn,结合不等式可求n的值.
解:由an=2n-1可得数列{an}为等差数列
∴a1=1
∴Sn=
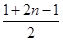 ?n=n2>48
?n=n2>48∵n∈N*
∴使Sn>48成立的n的最小值为n=7
故选A.

练习册系列答案
相关题目
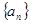 中,
中,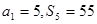 ,则公比
,则公比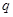 等于 ( )
等于 ( )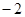
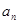 }中,
}中,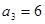 ,前三项和
,前三项和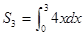 ,则公比
,则公比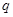 =( )
=( ) 
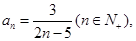 记数列
记数列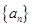 的前
的前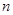 项和为
项和为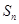 ,即
,即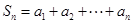 ,则使
,则使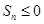 的
的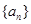 满足
满足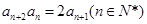 ,且
,且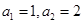 ,则数列
,则数列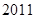 项的乘积为
项的乘积为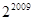
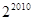
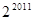
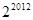
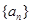 满足
满足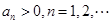 ,且
,且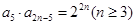 ,则当
,则当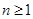
 ( )
( ) 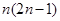
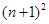
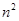
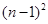
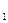 =1,a
=1,a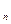 =a
=a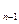 +3(n≥2,n∈N
+3(n≥2,n∈N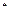 ),则a
),则a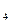 ="( " )
="( " ) 中,
中, 则前11项的和
则前11项的和 = .
= .
 中,已知
中,已知 ,
, ,
, ,…,
,…, ,则
,则 的最大值为______________.
的最大值为______________.