题目内容
20.(本小题满分8分)如图,AB是⊙O的直径,PA⊥⊙O所在的平面,C是圆上一点,∠ABC = 30°,PA = AB.
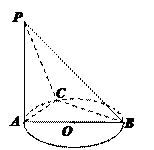 (1)求证:平面PAC⊥平面PBC;
(1)求证:平面PAC⊥平面PBC;
(2)求直线PC与平面ABC所成角的正切值;
(3)求二面角A—PB—C的正弦值.
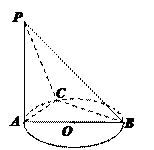 (1)求证:平面PAC⊥平面PBC;
(1)求证:平面PAC⊥平面PBC;(2)求直线PC与平面ABC所成角的正切值;
(3)求二面角A—PB—C的正弦值.
解:(1)证明:∵AB是直径 ∴∠ACB = 90°,即BC⊥AC
∴PA⊥BC
∴BC⊥平面PAC 又BC 平面PBC
平面PBC
∴平面PBC⊥平面PAC
(2)∵PA⊥平面ABC
∴直线PC与平面ABC所成角即∠PCA
设AC = 1,∵∠ABC = 30°∴PA = AB = 2
∴tan∠PCA = = 2
(3) 在平面PAC中作AD⊥PC于D,在平面PAB中作AE⊥PB于连结DE
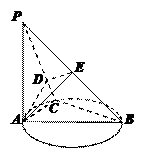 ∵平面PAC⊥平面PBC,平面PAC∩平面PBC = PC,AD⊥PC
∵平面PAC⊥平面PBC,平面PAC∩平面PBC = PC,AD⊥PC
∴AD⊥平面PBC
∴AD⊥PB
又∵PB⊥AE ∴PB⊥面AED
∴PB⊥ED
∴∠DEA即为二面角A—PB—C的平面角
在直角三角形PAC中和直角三角形PAB中,
分别由等面积方法求得
AD = AE =
∴在直角三角形ADE中可求得:sin∠DEA =
即二面角A—PB—C的正弦值为.
∴PA⊥BC
∴BC⊥平面PAC 又BC
 平面PBC
平面PBC∴平面PBC⊥平面PAC
(2)∵PA⊥平面ABC
∴直线PC与平面ABC所成角即∠PCA
设AC = 1,∵∠ABC = 30°∴PA = AB = 2
∴tan∠PCA = = 2
(3) 在平面PAC中作AD⊥PC于D,在平面PAB中作AE⊥PB于连结DE
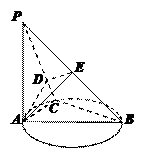 ∵平面PAC⊥平面PBC,平面PAC∩平面PBC = PC,AD⊥PC
∵平面PAC⊥平面PBC,平面PAC∩平面PBC = PC,AD⊥PC∴AD⊥平面PBC
∴AD⊥PB
又∵PB⊥AE ∴PB⊥面AED
∴PB⊥ED
∴∠DEA即为二面角A—PB—C的平面角
在直角三角形PAC中和直角三角形PAB中,
分别由等面积方法求得
AD = AE =
∴在直角三角形ADE中可求得:sin∠DEA =
即二面角A—PB—C的正弦值为.
略

练习册系列答案
相关题目

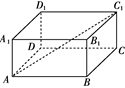
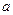 的正方体
的正方体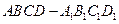 中,
中,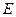 是线段
是线段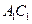 的中点,
的中点,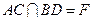 .
.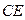 ^
^ ;
;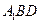 ;
;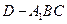 的体积.
的体积.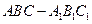 ,在某个空间直角坐标系中,
,在某个空间直角坐标系中, ,
,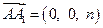 ,其中
,其中 、
、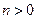

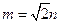 ,求直线
,求直线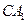 与平面
与平面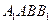 所成角的大小。
所成角的大小。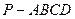 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 =2,
=2,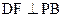 ,垂足为F。
,垂足为F。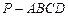 中,底面
中,底面 是平行四边形,
是平行四边形,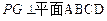 ,垂足为
,垂足为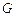 ,
,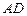 上,且
上,且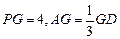 ,
,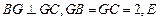 是
是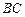 的中点.
的中点.
 与
与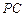 所成的角的余弦值;
所成的角的余弦值;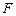 是棱
是棱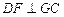 ,求
,求 的值.
的值.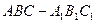 中
中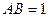 ,
,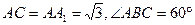
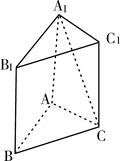
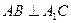
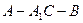 的大小
的大小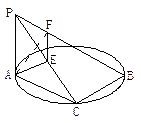
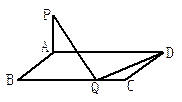
 (第20题) (第21题)
(第20题) (第21题)