题目内容
如图a,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线EF把四边形CDFE折起如图b,使平面CDFE⊥平面ABEF.
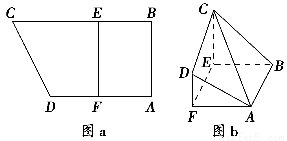
(1)求证:AB⊥平面BCE;
(2)求三棱锥C ?ADE体积.
(1)见解析 (2)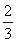
【解析】
(1)证明:在题图a中,EF∥AB,AB⊥AD,
∴EF⊥AD,在题图b中,CE⊥EF,又平面CDFE⊥平面ABEF,且平面CDFE∩平面ABEF=EF,
CE⊥平面ABEF,AB?平面ABEF,∴CE⊥AB,又∵AB⊥BE,BE∩CE=E,∴AB⊥平面BCE;
(2)解:∵平面CDFE⊥平面ABEF,且平面CDFE∩平面ABEF=EF,AF⊥FE,AF?平面ABEF,∴AF⊥平面CDEF,∴AF为三棱锥A ?CDE的高,且AF=1,又∵AB=CE=2,∴S△CDE=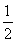 ×2×2=2,
×2×2=2,
∴VC ?ADE=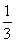 ·S△CDE·AF=
·S△CDE·AF=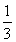 ×2×1=
×2×1=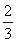 .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目