��Ŀ����
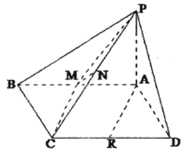
����Ŀ��ijѧУ��ƽ��ͼΪ���εIJٳ�ABCD�ڽ�����ٱ��ݣ�����AB��40��BC��15��OΪAB��һ�㣬��BO��10���߶�OC��OD��MNΪ���ݶ�������λ�ã�M��N�ֱ����߶�OD��OC�ϣ�����OCD�ڵĵ�PΪ���λ�ã���P��OC��OD�ľ���ֱ�Ϊ![]() ��
��![]() ����OM��d������֪������OMN�����Сʱ����Ч����ã�
����OM��d������֪������OMN�����Сʱ����Ч����ã�
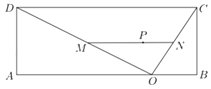
��1����dΪ��ֵʱ��PΪ����MN���е㣻
��2����������M��λ�ò���ʹ����Ч����ã������ʱ��OMN�������
���𰸡�(1)![]() ��(2) M��N��P ���㹲�ߣ����Ϊ
��(2) M��N��P ���㹲�ߣ����Ϊ![]() ��
��
��������
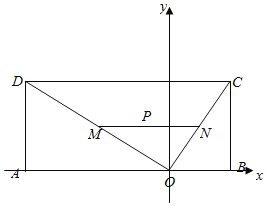
1����OΪ����ԭ�㣬AB����ֱ��Ϊx�ᣬ��O��ֱ��AB��ֱ��Ϊy�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ��OC��y��1.5x��OD��y����0.5x����P��a��b����M����2m��m����N��n��1.5n������m��0��n��0������⼴��
��2��ͨ��![]() �Ƴ�
�Ƴ�![]() �����û�������ʽ�Լ������������ʽ����
�����û�������ʽ�Լ������������ʽ����
��1����OΪ����ԭ�㣬AB����ֱ��Ϊx�ᣬ��O��ֱ��AB��ֱ��Ϊy�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����C��10��15����B��10��0����D����30��15����P����4��4����OC��y��1.5x��OD��y����0.5x��
��P��a��b����M����2m��m����N��n��1.5n������m��0��n��0����
P��OC��OD�ľ���ֱ�Ϊ![]() ��
��![]() �������ⷽ����
�������ⷽ����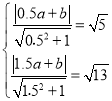 ����
����![]() ��
��
��PΪMN���е㣬����![]() ����m
����m![]() ��n
��n![]() ������
������![]() ��
��
��d��|OM|![]() ��
��
��2����M��N��P ���㹲�ߣ���![]() ��5m+6.5n��4mn����
��5m+6.5n��4mn����![]() ��
��
S��OMN![]() ��
��
��2m+n��![]() �����ҽ���5n2��13m2������
�����ҽ���5n2��13m2������
���ԡ�OMN�����СΪ![]() ��
��

����Ŀ�����幺����Ʊ��Ʊ�����±���
��Ʊ���� | 1~50 | 51~100 | 100���� |
��Ʊ�۸� | 13Ԫ/�� | 11Ԫ/�� | 9Ԫ/�� |
��ij��λҪ��֯���г�������������Ա�������ù������������������ֱ�Ϊa��b![]() ������������Ϊ���壬ѡ��������ͬ��ʱ��ֱ�Ʊ������������֧����Ʊ��Ϊ1290Ԫ�����������ź���һ����Ϊһ�����壬ͬһʱ�乺Ʊ������������֧����Ʊ��Ϊ990Ԫ����ô���������ŵ�����
������������Ϊ���壬ѡ��������ͬ��ʱ��ֱ�Ʊ������������֧����Ʊ��Ϊ1290Ԫ�����������ź���һ����Ϊһ�����壬ͬһʱ�乺Ʊ������������֧����Ʊ��Ϊ990Ԫ����ô���������ŵ�����![]() ____��
____��![]() ____.
____.