题目内容
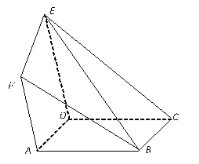
【题目】如图,在多面体![]() 中,底面
中,底面![]() 为矩形,侧面
为矩形,侧面![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)判断线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?并说明理由.
?并说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)见证明;(Ⅲ)见解析
【解析】
(I)由AD⊥DE,AD⊥CD可得AD⊥平面CDE,故而AD⊥CE;
(II)证明平面ABF∥平面CDE,故而BF∥平面CDE;
(III)取CE的中点P,BE的中点Q,证明CE⊥平面ADPQ即可得出平面ADQ⊥平面BCE.
(Ⅰ)由底面![]() 为矩形,知
为矩形,知![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() .
.

(Ⅱ)由底面![]() 为矩形,知
为矩形,知![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() ,
,
又因为![]() ,
,
所以平面![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅲ)结论:线段![]() 上存在点
上存在点![]() (即
(即![]() 的中点),使得平面
的中点),使得平面![]() 平面
平面![]() .
.
证明如下:
取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() .
.
由![]() ,得
,得![]() .
.
所以![]() 四点共面.
四点共面.
由(Ⅰ),知![]() 平面
平面![]() ,
,
所以![]() ,故
,故![]() .
.
在△![]() 中,由
中,由![]() ,可得
,可得![]() .
.
又因为![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]()
所以平面![]() 平面
平面![]() (即平面
(即平面![]() 平面
平面![]() ).
).
即线段![]() 上存在点
上存在点![]() (即
(即![]() 中点),使得平面
中点),使得平面![]() 平面
平面![]()

练习册系列答案
相关题目
【题目】某电子商务平台的管理员随机抽取了1000位上网购物者,并对其年龄(在10岁到69岁之间)进行了调查,统计情况如下表所示.
年龄 |
|
|
|
|
|
|
人数 | 100 | 150 |
| 200 |
| 50 |
已知![]() ,
,![]() ,
,![]() 三个年龄段的上网购物的人数依次构成递减的等比数列.
三个年龄段的上网购物的人数依次构成递减的等比数列.
(1)求![]() 的值;
的值;
(2)若将年龄在![]() 内的上网购物者定义为“消费主力军”,其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,再从这5人中抽取2人,求这2人中至少有一人是消费潜力军的概率.
内的上网购物者定义为“消费主力军”,其他年龄段内的上网购物者定义为“消费潜力军”.现采用分层抽样的方式从参与调查的1000位上网购物者中抽取5人,再从这5人中抽取2人,求这2人中至少有一人是消费潜力军的概率.