题目内容
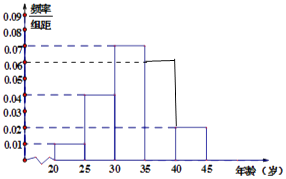
【题目】当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：
组数 | 分组（单位：岁） | 频数 | 频率 |
1 | [20，25） | 5 | 0.05 |
2 | [25，30） | 20 | 0.20 |
3 | [30，35） | a | 0.35 |
4 | [35，40） | 30 | b |
5 | [40，45] | 10 | 0.10 |
合计 | n | 1.00 | |
（1）求出表中的a，b，n的值，并补全频率分布直方图；
（2）媒体记者为了做好调查工作，决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访，再从抽出的这20名中年龄在[30，40）的选取2名担任主要发言人．记这2名主要发言人年龄在[35，40）的人数为ξ，求ξ的分布列及数学期望．
【答案】
（1）解：由题意可得：n= 
=100，∴a=100×0.35=35，b= 
=0.3．
如图所示，
（2）按年龄采用分层抽样的方法在[30，35），
（35，40]分别有m，n名，可得： 
= 
= 
，
解得m=7，n=6，
∴年龄在[30，40）共有13名．故ξ的可能取值为0，1，2．利用P（ξ=k）= 
，可得：P（ξ=0）= 
，
P（ξ=1）= 
，P（ξ=2）= 
．
∴ξ的分布列为：
ξ | 0 | 1 | 2 |
P | | | |
Eξ=0× +1× +2× = 
．
【解析】（1）由题意可得：n= =100，可得a=100×0.35，b= ．（2）按年龄采用分层抽样的方法在[30，35），（35，40]分别有m，n名，可得： = = ，解得m，n，可得年龄在[30，40）共有13名．故的可能取值为0，1，2．利用P（ξ=k）= ，即可得出分布列与数学期望．
【考点精析】通过灵活运用离散型随机变量及其分布列，掌握在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列即可以解答此题．
