题目内容
已知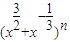 的展开式中各项系数的和是128,则展开式中x5的系数是 .(以数字作答)
的展开式中各项系数的和是128,则展开式中x5的系数是 .(以数字作答)
【答案】分析:通过对二项式中的x赋值1求出展开式的各项系数和,列方程求出n;利用二项展开式的通项公式求出第r+1项,令x的指数为5,求出展开式中x5的系数.
解答:解:∵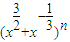 的展开式中各项系数和为128,
的展开式中各项系数和为128,
∴令x=1,即得所有项系数和为2n=128.
∴n=7.
设该二项展开式中的第r+1项为Tr+1=C7r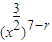 •
•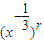 =C7r•
=C7r•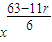 ,
,
令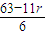 =5即r=3时,
=5即r=3时,
∴x5项的系数为C73=35.
故答案为35
点评:本题考查赋值法是求展开式的各项系数和的重要方法,考查二项展开式的通项公式是解决二项展开式的特定项问题的工具.
解答:解:∵
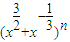 的展开式中各项系数和为128,
的展开式中各项系数和为128,∴令x=1,即得所有项系数和为2n=128.
∴n=7.
设该二项展开式中的第r+1项为Tr+1=C7r
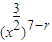 •
•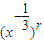 =C7r•
=C7r•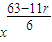 ,
,令
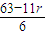 =5即r=3时,
=5即r=3时,∴x5项的系数为C73=35.
故答案为35
点评:本题考查赋值法是求展开式的各项系数和的重要方法,考查二项展开式的通项公式是解决二项展开式的特定项问题的工具.

练习册系列答案
相关题目