题目内容
已知函数 .
.
(1)当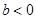 时,求
时,求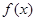 的单调区间;
的单调区间;
(2)当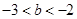 时,若存在
时,若存在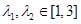 , 使得
, 使得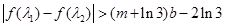 成立,求实数
成立,求实数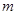 的取值范围.
的取值范围.
 .
.(1)当
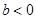 时,求
时,求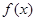 的单调区间;
的单调区间;(2)当
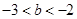 时,若存在
时,若存在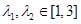 , 使得
, 使得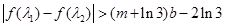 成立,求实数
成立,求实数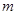 的取值范围.
的取值范围.(1)当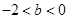 时,函数
时,函数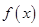 的单调递减区间为
的单调递减区间为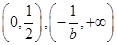 ,函数
,函数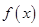 的单调递增区间为
的单调递增区间为 ;
;
当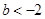 时,函数
时,函数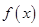 的单调递减区间为
的单调递减区间为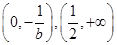 ,函数
,函数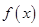 的单调递增区间为
的单调递增区间为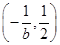 ;
;
当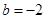 时,函数
时,函数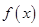 的单调递减区间为
的单调递减区间为 .
.
(2)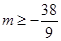
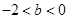 时,函数
时,函数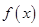 的单调递减区间为
的单调递减区间为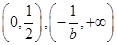 ,函数
,函数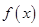 的单调递增区间为
的单调递增区间为 ;
;当
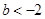 时,函数
时,函数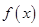 的单调递减区间为
的单调递减区间为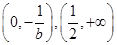 ,函数
,函数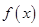 的单调递增区间为
的单调递增区间为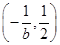 ;
;当
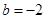 时,函数
时,函数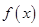 的单调递减区间为
的单调递减区间为 .
.(2)
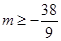
试题分析:(1)求函数
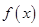 的导数
的导数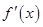 ,并利用导函数求
,并利用导函数求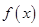 的单调区间,注意对参变量
的单调区间,注意对参变量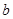 的取值进行分类讨论;
的取值进行分类讨论;(2)由(1)知,当
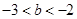 时,函数
时,函数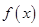 在
在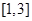 上单调递减,
上单调递减,
而原问题可等价转化为
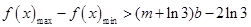
所以可先利用
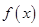 在
在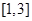 上单调递减,求出
上单调递减,求出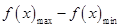 ,再用分离变量法求出实数
,再用分离变量法求出实数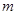 的取值范围.
的取值范围.解:(1)依题意,
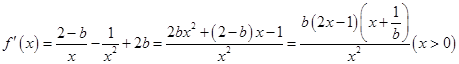 2分
2分当
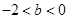 时,
时,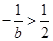 ,令
,令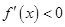 ,得
,得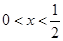 或
或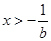
令
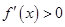 ,得
,得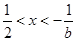 3分
3分当
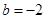 时,
时,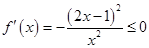 4分
4分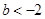 时,
时,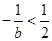 ,令
,令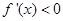 ,得
,得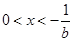 或
或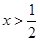 ;令
;令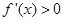 ,得
,得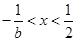 ;
;5分
综上所述:当
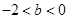 时,函数
时,函数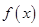 的单调递减区间为
的单调递减区间为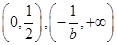 ,函数
,函数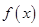 的单调递增区间为
的单调递增区间为 ;
;当
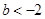 时,函数
时,函数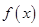 的单调递减区间为
的单调递减区间为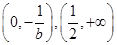 ,函数
,函数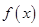 的单调递增区间为
的单调递增区间为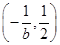 ;
;当
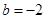 时,函数
时,函数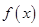 的单调递减区间为
的单调递减区间为 6分 .
6分 .(2) 由(1)知,当
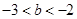 时,函数
时,函数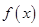 在
在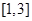 上单调递减,
上单调递减,所以
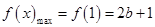 ,
,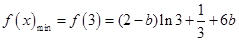 7分
7分所以,
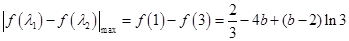 8分
8分因为存在
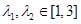 ,使得
,使得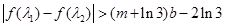 成立
成立所以

整理得:
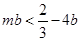 10分
10分又
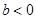 ,所以
,所以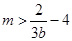 ,又因为
,又因为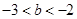 ,得
,得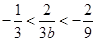 ,
,所以
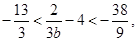 所以
所以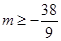 12分
12分
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
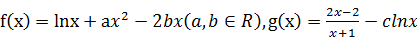 .
.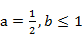 时,
时,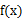 与
与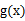 )在定义域上单调性相反,求的
)在定义域上单调性相反,求的 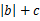 的最小值。
的最小值。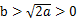 时,求证:存在
时,求证:存在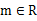 ,使
,使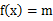 的三个不同的实数解
的三个不同的实数解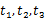 ,且对任意
,且对任意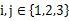 且
且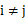 都有
都有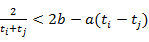 .
. ,函数
,函数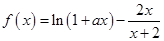 .
.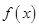 在区间
在区间 上的单调性;
上的单调性;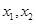 ,且
,且 ,求
,求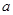 的取值范围.
的取值范围.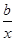 ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.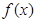 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为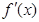 ,且有
,且有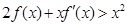 ,则不等式
,则不等式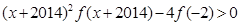 的解集为( )
的解集为( )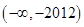
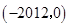

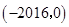
 ,则
,则 = .
= . 在
在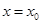 处取最大值。以下各式正确的序号为 .
处取最大值。以下各式正确的序号为 .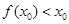 ②
②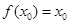 ③
③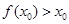 ④
④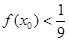 ⑤
⑤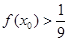
 上的连续函数
上的连续函数 的导函数为
的导函数为 ,如果
,如果 使得
使得 ,则称
,则称 为区间
为区间 ;②
;② ;③
;③ ;④
;④ 在区间
在区间 上“中值点”多于一个的函数序号为 .
上“中值点”多于一个的函数序号为 .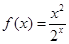 在区间
在区间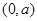 内单调,则
内单调,则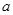 的最大值为__________.
的最大值为__________.