题目内容
定义在区间 上的连续函数
上的连续函数 的导函数为
的导函数为 ,如果
,如果 使得
使得 ,则称
,则称 为区间
为区间 上的“中值点”.下列函数:①
上的“中值点”.下列函数:① ;②
;② ;③
;③ ;④
;④ 在区间
在区间 上“中值点”多于一个的函数序号为 .
上“中值点”多于一个的函数序号为 .
 上的连续函数
上的连续函数 的导函数为
的导函数为 ,如果
,如果 使得
使得 ,则称
,则称 为区间
为区间 上的“中值点”.下列函数:①
上的“中值点”.下列函数:① ;②
;② ;③
;③ ;④
;④ 在区间
在区间 上“中值点”多于一个的函数序号为 .
上“中值点”多于一个的函数序号为 .①④
试题分析:根据“中值点”的定义,设
 为区间
为区间 上的中值点,则
上的中值点,则 ,①中
,①中 ,因为
,因为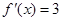 ,此时区间
,此时区间 的任一实数都为“中值点”;对于②,
的任一实数都为“中值点”;对于②, 即
即 ;对于③
;对于③ 即
即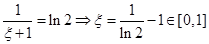 ;对于④
;对于④ 即
即 ;综上可知,选①④.
;综上可知,选①④.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
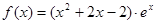 ,
,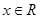 ,
,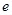 为自然对数的底数.
为自然对数的底数.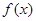 的极值;
的极值;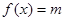 有两个不同的实数根,试求实数
有两个不同的实数根,试求实数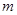 的取值范围;
的取值范围;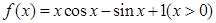 .
. 的单调区间;
的单调区间; 为
为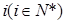 个零点,证明:对一切
个零点,证明:对一切 ,有
,有 .
. .
.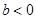 时,求
时,求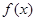 的单调区间;
的单调区间;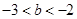 时,若存在
时,若存在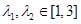 , 使得
, 使得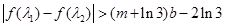 成立,求实数
成立,求实数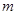 的取值范围.
的取值范围.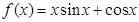 的导函数原点处的部分图象大致为 ( )
的导函数原点处的部分图象大致为 ( )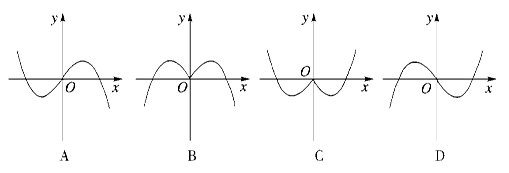
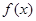 在R上可导,
在R上可导, ,则
,则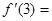 ( )
( )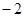
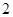
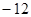
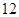
 ,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于________.
,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于________.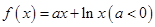 .
.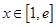 时,函数
时,函数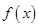 的最大值为
的最大值为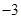 ,求
,求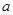 的值;
的值;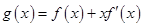 (
(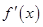 为函数
为函数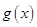 在
在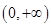 上是单调函数,求
上是单调函数,求