题目内容
8.已知数列{an}的前n项和Sn=$\frac{1}{2}$anan+1,n∈N*,且a1=1.(1)求数列{an}的通项公式;
(2)设bn=$\frac{2n-1}{{2}^{{a}_{n}}}$(n∈N*),数列{bn}的前n项和为Tn,写出Tn关于n表达式,并求满足Tn>$\frac{5}{2}$时n的取值范围.
分析 (1)利用递推关系与等差数列的通项公式即可得出;
(2)利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(1)∵数列{an}的前n项和Sn=$\frac{1}{2}$anan+1,n∈N*,且a1=1.
∴当n=1时,a1=$\frac{1}{2}{a}_{1}{a}_{2}$,解得a2=2.
当n≥2时,an=Sn-Sn-1=$\frac{1}{2}$anan+1-$\frac{1}{2}{a}_{n-1}{a}_{n}$=$\frac{1}{2}{a}_{n}({a}_{n+1}-{a}_{n-1})$.
化为an(an+1-an-1-2)=0,
an≠0,可得an+1-an-1=2.
∴数列{an}的奇数项与偶数项分别成等差数列,公差为2,首项分别为1,2.
∴an+1-an+(an-an-1)=2,
∴an-an-1=1,
∴数列{an}是等差数列,公差为1,首项为1.
an=1+(n-1)=n.
(2)bn=$\frac{2n-1}{{2}^{{a}_{n}}}$=$\frac{2n-1}{{2}^{n}}$(n∈N*),
∴数列{bn}的前n项和为Tn=$\frac{1}{2}+\frac{3}{{2}^{2}}$+…+$\frac{2n-1}{{2}^{n}}$,
$\frac{1}{2}{T}_{n}$=$\frac{1}{{2}^{2}}+\frac{3}{{2}^{3}}$+…+$\frac{2n-3}{{2}^{n}}$+$\frac{2n-1}{{2}^{n+1}}$,
∴$\frac{1}{2}{T}_{n}$=$\frac{1}{2}+2×(\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}})$-$\frac{2n-1}{{2}^{n+1}}$=1+$\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-$\frac{1}{2}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-$\frac{1}{2}$-$\frac{2n-1}{{2}^{n+1}}$=$\frac{3}{2}$-$\frac{2n+3}{{2}^{n+1}}$,
∴${T}_{n}=3-\frac{2n+3}{{2}^{n}}$.
不等式Tn>$\frac{5}{2}$,
即$\frac{1}{2}>\frac{2n+3}{{2}^{n}}$,
由于$\frac{2n+3}{{2}^{n}}$-$\frac{2(n+1)+3}{{2}^{n+1}}$=$\frac{2n+1}{{2}^{n+1}}$>0,
∴数列$\{\frac{2n+3}{{2}^{n}}\}$为单调递减数列,
当n=4时,$\frac{11}{16}$$>\frac{1}{2}$;当n=5时,$\frac{13}{32}$$<\frac{1}{2}$.
∴满足Tn>$\frac{5}{2}$时n的取值范围是n≥5.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式、不等式的性质,考查了推理能力与计算能力,属于中档题.

| A. | 25 | B. | 16 | C. | 14 | D. | 12 |
| A. | [0,1] | B. | [1,7] | C. | [7,9] | D. | [9,21] |
| A. | y=|sinx| | B. | y=sin|x| | C. | y=sinx | D. | y=$\frac{1}{2}$sinx |
| A. | A | B. | ∅ | C. | B | D. | {-2,-1,0,2} |
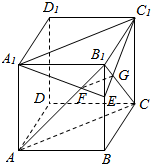 如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.
如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.