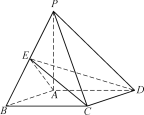
题目内容
【题目】如图1，直线
将矩形
分为两个直角梯形
和
，将梯形沿边翻折，如图2，在翻折过程中（平面和平面不重合），下列说法正确的是（ ）
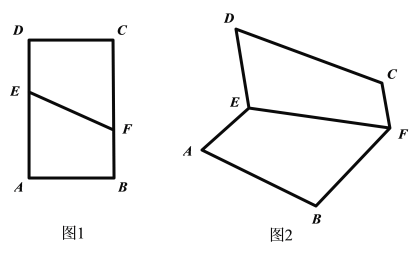
A.存在某一位置，使得
平面
B.存在某一位置，使得
平面
C.存在某一位置，使得
D.在翻折过程中，恒有直线
平面
【答案】D
【解析】
根据线线、线面、面面有关定理，对选项逐一分析，由此确定正确选项.
对于A选项，假设存在某一位置，使得
平面
，由于平面
平面
，根据线面平行的性质定理有
，由图可知这与四边形
是直角梯形矛盾，故A选项错误.
对于B选项，假设存在某一位置，使得
平面，则
，由图可知这与四边形是直角梯形矛盾，故B选项错误.
对于C选项，根据异面直线的知识可知，
与
是异面直线，故C选项错误.
对于D选项，由于
，所以平面
平面
，所以在翻折过程中，恒有直线
平面.
故选：D
【题目】2019年4月，甲乙两校的学生参加了某考试机构举行的大联考，现对这两校参加考试的学生的数学成绩进行统计分析，数据统计显示，考生的数学成绩
服从正态分布
，从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷，并将这40份试卷的得分制作成如图所示的茎叶图：
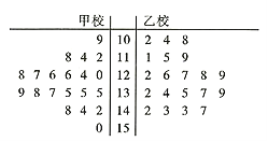
（1）试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数；
（2）若把数学成绩不低于135分的记作数学成绩优秀，根据茎叶图中的数据，判断是否有
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关？
（3）从所有参加此次联考的学生中（人数很多）任意抽取3人，记数学成绩在134分以上的人数为
，求的数学期望．
附：若随机变量服从正态分布
，则
，
，
．
参考公式与临界值表：
，其中
．
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动，为了解小朋友坚持打卡的情况，对该幼儿园所有小朋友进行了调查，调查结果如下表：
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
（1）根据上表数据，求该幼儿园男生平均打卡的天数；
（2）若从打卡21天的小朋友中任选2人交流心得，求选到男生和女生各1人的概率.
