题目内容

19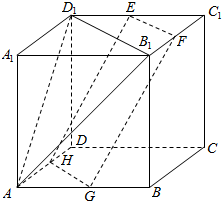．在正方体ABCD-A1B1C1D1中，E，F，G，H分别是棱D1C1，B1C1，AB，AD的中点，求证：平面D1B1A∥平面EFGH．

分析 连结HF，由已知条件推导出EF∥D1B1，B1F$\underset{∥}{=}$AH，由此能证明平面D1B1A∥平面EFGH．

解答 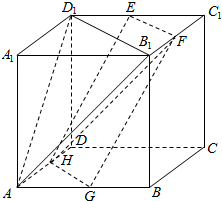证明：连结HF，∵在正方体ABCD-A1B1C1D1中，E，F，G，H分别是棱D1C1，B1C1，AB，AD的中点，
∴EF∥D1B1，B1F$\underset{∥}{=}$AH，∴四边形AHFB1是平行四边形，
∴HF∥AB1，
∵EF∩FG=F，D1B1∩B1A=B1，
EF?平面EFGH，FG?平面EFGH，D1B1?平面D1B1A，AB1?平面D1B1A，
∴平面D1B1A∥平面EFGH．

点评 本题考查面面平行的证明，是基础题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．

练习册系列答案
相关题目
9．已知函数f（x）=ex，g（x）=x2-ax+1．
（Ⅰ）若函数y=f（x）+g（x）在区间[1，+∞）上单调递增，求实数a的取值范围；
（Ⅱ） 记h（x）=$\frac{f（x）}{g（x）}$，若$a∈[{0，\frac{1}{2}}]$，则当x∈[0，a+1]时，函数h（x）的图象是否总在不等式y＞x所表示的平面区域内，请写出判断过程．
10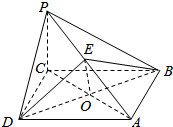．如图所示，已知P是边长为a的菱形ABCD所在平面外一点，∠ABC=60°，PC⊥平面ABCD，PC=a，E为PA的中点．
（1）求证：平面EDB⊥平面ABCD；
（2）求二面角A-EB-D的正切值．
7．某几何体的三视图如图所示，则该几何体的表面积为19+$\sqrt{5}$．
14．四边形ABCD是矩形，P为平面ABCD外一点，PA⊥平面ABCD，且PA=AB，则二面角P-BC-D的大小为45°．
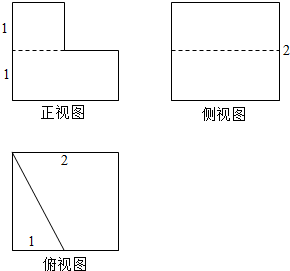
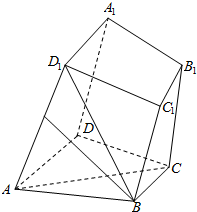4．如图所示，四棱柱ABCD-A1B1C1D1中，底面ABCD是梯形，AD∥BC，侧面ABB1A1为菱形，∠DAB=∠DAA1
（1）求证：A1B⊥AD1；
（2）若AD=AB=2BC，点D在平面ABB1A1上的射影恰为线段A1B的中点，∠A1AB=60°，求平面DCC1D1与平面ABB1A1所成锐二面角的余弦值．
11．在正方体ABCD-A1B1C1D1中，过AB、AD、DD1的中点P、Q、R作截面，求截面与面CC1D1D所成的二面角的大小．
8．求证：$\frac{|a|+|b|}{1+|a|+|b|}$≥$\frac{|a+b|}{1+|a+b|}$．
9．如图，两曲线y=3-x2与y=x2-2x-1所围成的图形面积是（　　）
A．6B．9C．12D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网