题目内容
8.求证:$\frac{|a|+|b|}{1+|a|+|b|}$≥$\frac{|a+b|}{1+|a+b|}$.分析 通过作差、利用|a|+|b|≥|a+b|,整理即得结论.
解答 证明:$\frac{|a|+|b|}{1+|a|+|b|}$-$\frac{|a+b|}{1+|a+b|}$
=$\frac{1}{(1+|a|+|b|)(1+|a+b|)}$[(|a|+|b|)(1+|a+b|)-(1+|a|+|b|)|a+b|]
=$\frac{1}{(1+|a|+|b|)(1+|a+b|)}$[|a|+|b|+|a+b|•|a|+|a+b|•|b|-(|a+b|+|a+b|•|a|+|a+b|•|b|)]
=$\frac{1}{(1+|a|+|b|)(1+|a+b|)}$(|a|+|b|-|a+b|)
≥0,
∴$\frac{|a|+|b|}{1+|a|+|b|}$≥$\frac{|a+b|}{1+|a+b|}$.
点评 本题考查不等式的证明,利用作差法是解决本题的关键,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
3.设F2(c,0)(c>0)是双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,M是双曲线左支上的一点,线段MF2与圆x2+y2-$\frac{2c}{3}$x+$\frac{{a}^{2}}{9}$=0相切于D,且|MF2|=3|DF2|,则双曲线Γ的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
13.已知F1、F2分别是双曲线x2-$\frac{{y}^{2}}{6}$=1的左、右焦点,点P为右支上一点,O为坐标原点,若向量($\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$)与$\overrightarrow{P{F}_{2}}$的夹角为120°,则点F2到直线PF1的距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{21}$ |
20.已知集合U={1,2,3,4},A={1},B={2,4},则A∪(∁UB)=( )
| A. | {1} | B. | {3} | C. | {1,3} | D. | {1,2,3} |
17.若函数f(x2+1)的定义域为[-1,1],则f(lgx)的定义域为( )
| A. | [-1,1] | B. | [1,2] | C. | [10,100] | D. | [0,lg2] |
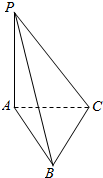 如图,PA⊥平面ABC,∠ACB=90°,AB=$\sqrt{2}$,PA=BC=1,求二面角P-BC-A的大小.
如图,PA⊥平面ABC,∠ACB=90°,AB=$\sqrt{2}$,PA=BC=1,求二面角P-BC-A的大小.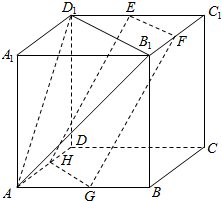 在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱D1C1,B1C1,AB,AD的中点,求证:平面D1B1A∥平面EFGH.
在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱D1C1,B1C1,AB,AD的中点,求证:平面D1B1A∥平面EFGH. 在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.
在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.