题目内容
11.在正方体ABCD-A1B1C1D1中,过AB、AD、DD1的中点P、Q、R作截面,求截面与面CC1D1D所成的二面角的大小.分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出截面与面CC1D1D所成的二面角的大小.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1棱长为2,
则Q(1,0,0),R(0,0,1),P(1,1,0),
$\overrightarrow{QR}$=(-1,0,1),$\overrightarrow{QP}$=(0,1,0),
设平面PQR的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{QR}=-x+z=0}\\{\overrightarrow{n}•\overrightarrow{QP}=y=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
平面CC1D1D的法向量$\overrightarrow{m}$=(1,0,0),
cos<$\overrightarrow{n},\overrightarrow{m}$>=|$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}|•|\overrightarrow{m}|}$|=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴截面与面CC1D1D所成的二面角的大小为$\frac{π}{4}$.
点评 本题考查二面角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
1.已知函数f(x)的值域是[-2,3],则函数f(x-2)的值域为( )
| A. | [-4,1] | B. | [0,5] | C. | [-4,1]∪[0,5] | D. | [-2,3] |
3.设F2(c,0)(c>0)是双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,M是双曲线左支上的一点,线段MF2与圆x2+y2-$\frac{2c}{3}$x+$\frac{{a}^{2}}{9}$=0相切于D,且|MF2|=3|DF2|,则双曲线Γ的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
20.已知集合U={1,2,3,4},A={1},B={2,4},则A∪(∁UB)=( )
| A. | {1} | B. | {3} | C. | {1,3} | D. | {1,2,3} |
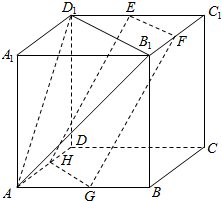 在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱D1C1,B1C1,AB,AD的中点,求证:平面D1B1A∥平面EFGH.
在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱D1C1,B1C1,AB,AD的中点,求证:平面D1B1A∥平面EFGH. 在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.
在四棱锥P-ABCD中,∠ABC=$\frac{π}{2}$,∠BAC=∠CAD=$\frac{π}{3}$,PA⊥平面ABCD,E为PD的中点,PA=2AB=2,CD=2$\sqrt{3}$.