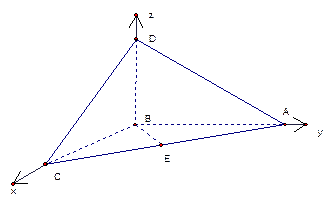
题目内容
已知在长方体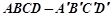 中,点
中,点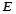 为棱
为棱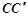 上任意一点,
上任意一点,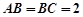 ,
,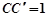 .
.
(Ⅰ)求证:平面
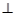 平面
平面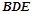 ;
;
(Ⅱ)若点 为棱
为棱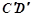 的中点,点
的中点,点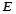 为棱
为棱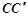 的中点,求二面角
的中点,求二面角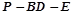 的余弦值.
的余弦值.
(Ⅰ)详见解析;(Ⅱ)二面角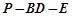 的余弦值为
的余弦值为 .
.
解析试题分析:(Ⅰ)求证:平面
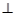 平面
平面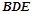 ,证明两个平面垂直,只需证明一个平面过另一个平面的垂线即可,由长方体的性质,易证
,证明两个平面垂直,只需证明一个平面过另一个平面的垂线即可,由长方体的性质,易证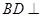 平面
平面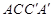 ,从而可证平面
,从而可证平面
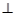 平面
平面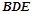 ;(Ⅱ)若点
;(Ⅱ)若点 为棱
为棱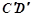 的中点,点
的中点,点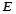 为棱
为棱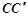 的中点,求二面角
的中点,求二面角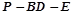 的余弦值,求二面角问题,可用传统方法,找二面角的平面角,但本题不易找,另一种方法,用向量法,本题因为是长方体,容易建立空间坐标系,以
的余弦值,求二面角问题,可用传统方法,找二面角的平面角,但本题不易找,另一种方法,用向量法,本题因为是长方体,容易建立空间坐标系,以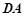 为
为 轴,以
轴,以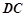 为
为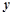 轴,以
轴,以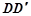 为
为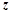 轴建立空间直角坐标系,分别设出两个平面的法向量,利用向量的运算,求出向量,即可求出二面角
轴建立空间直角坐标系,分别设出两个平面的法向量,利用向量的运算,求出向量,即可求出二面角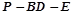 的余弦值.
的余弦值.
试题解析:(Ⅰ)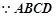 为正方形
为正方形  2分
2分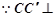 平面
平面
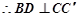 4分
4分
又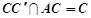 ,
,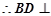 平面
平面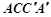
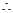 平面
平面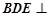 平面
平面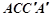 6分
6分
(Ⅱ)建立以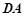 为
为 轴,以
轴,以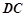 为
为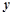 轴,以
轴,以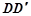 为
为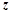 轴的空间直角坐标系 7分
轴的空间直角坐标系 7分
设平面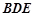 的法向量为
的法向量为 ,
,
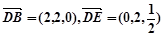
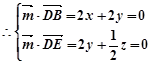
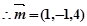 9分
9分
设平面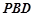 的法向量为
的法向量为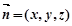 ,
,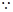

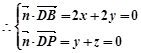
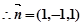 11分
11分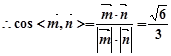 13分
13分 二面角
二面角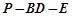 的余弦值为
的余弦值为 14分
14分
考点:面面垂直,二面角.

练习册系列答案
相关题目
 为矩形,
为矩形,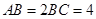 ,
,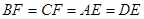 ,
,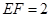 ,
,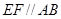 ,
,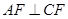 .
.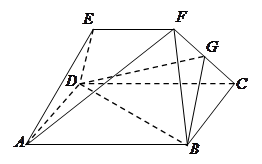
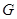 为
为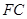 的中点,证明:
的中点,证明: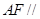 面
面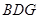 ;
;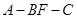 的余弦值.
的余弦值. ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.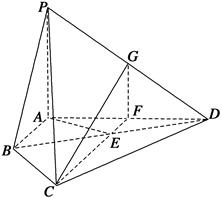
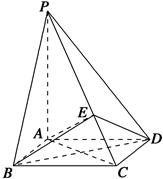
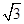 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.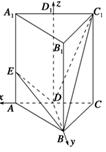
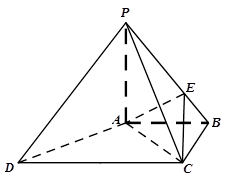
 中,
中, ⊥平面
⊥平面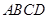 ,底面
,底面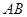 ∥
∥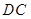 ,
,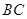 ,
,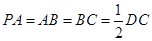 ,点
,点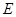 在棱
在棱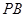 上,且
上,且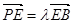 .
.
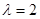 时,求证:
时,求证: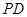 ∥面
∥面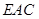 ;
;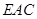 所成角为
所成角为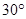 ,求实数
,求实数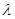 的值.
的值.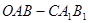 ,其中向量
,其中向量 ,三个向量之间的夹角均为
,三个向量之间的夹角均为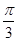 ,点
,点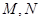 分别在
分别在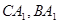 上且
上且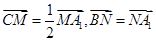 ,
,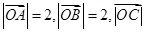 =4,如图
=4,如图
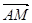 用向量
用向量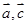 表示出来,并求
表示出来,并求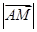 ;
;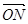 用
用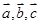 表示;
表示;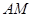 与
与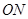 所成角的余弦值.
所成角的余弦值.
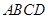 -
-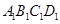 中,
中,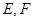 分别为
分别为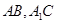 的中点. 应用空间向量方法求解下列问题.
的中点. 应用空间向量方法求解下列问题. 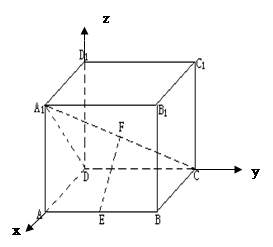
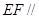 平面
平面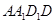 ;
;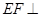 平面
平面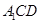 .
.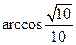 ,求BD的长度.(15分)
,求BD的长度.(15分)