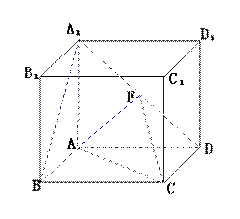
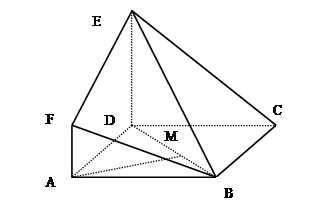
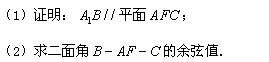题目内容
斜三棱柱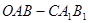 ,其中向量
,其中向量 ,三个向量之间的夹角均为
,三个向量之间的夹角均为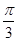 ,点
,点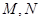 分别在
分别在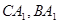 上且
上且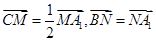 ,
,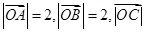 =4,如图
=4,如图
(Ⅰ)把向量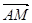 用向量
用向量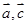 表示出来,并求
表示出来,并求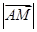 ;
;
(Ⅱ)把向量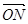 用
用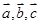 表示;
表示;
(Ⅲ)求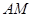 与
与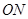 所成角的余弦值.
所成角的余弦值.
(Ⅰ) ,
,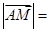
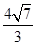 ;(Ⅱ)
;(Ⅱ)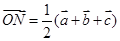 ;(Ⅲ)
;(Ⅲ)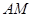 与
与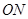 所成的角的余弦值
所成的角的余弦值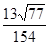 .
.
解析试题分析:(Ⅰ)把向量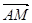 用向量
用向量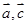 表示出来,像这一类题,先找以A为始点,以M为终点的封闭图形,因为向量
表示出来,像这一类题,先找以A为始点,以M为终点的封闭图形,因为向量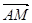 是用向量
是用向量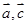 表示出来,而
表示出来,而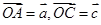 ,可在平面
,可在平面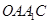 找,然后转化为与
找,然后转化为与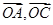 共线的向量,可求得,求
共线的向量,可求得,求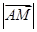 ,求向量的模,往往转化为模的平方来解,由
,求向量的模,往往转化为模的平方来解,由 ,故
,故 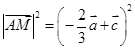 ,利用数量积展开,由
,利用数量积展开,由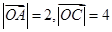 ,
,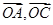 之间的夹角均为
之间的夹角均为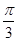 ,可求得
,可求得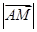 的值;(Ⅱ)把向量
的值;(Ⅱ)把向量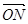 用
用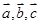 表示,和(Ⅰ)解题思想一样,只是他在空间中找;(Ⅲ)求
表示,和(Ⅰ)解题思想一样,只是他在空间中找;(Ⅲ)求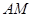 与
与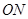 所成角的余弦值,利用
所成角的余弦值,利用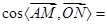
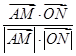 ,分别求出
,分别求出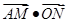 ,
,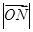 即可.
即可.
试题解析:(Ⅰ)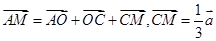 ,所以
,所以 ,因为
,因为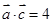 ,所以
,所以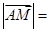
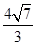
(Ⅱ)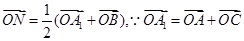 ,
,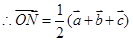
(Ⅲ)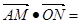
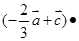
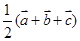 ,
,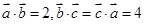
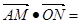
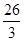 ,
,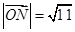 ,COS
,COS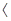
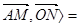
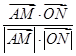 =
=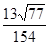 即为
即为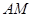 与
与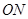 所成的角的余弦值.
所成的角的余弦值.
考点:向量加法与减法的几何意义,向量的夹角.

练习册系列答案
相关题目
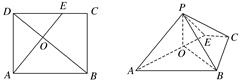
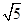 ,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=
,AD=6,BD是对角线,过点A作AE⊥BD,垂足为O,交CD于E,以AE为折痕将△ADE向上折起,使点D到点P的位置,且PB=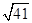 .
.
 为等腰直角三角形,
为等腰直角三角形, ,且
,且 .
.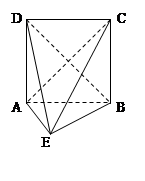
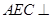 平面
平面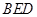 .
.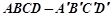 中,点
中,点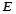 为棱
为棱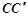 上任意一点,
上任意一点,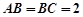 ,
,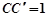 .
.

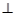 平面
平面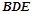 ;
; 为棱
为棱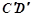 的中点,点
的中点,点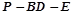 的余弦值.
的余弦值.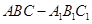 中,
中, ,
, ,
, 是
是 中点.
中点.
 平面
平面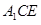 ;
; 与平面
与平面 是边长为3的正方形,
是边长为3的正方形, ,
,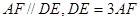 ,
,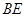 与平面
与平面 .
.
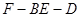 的的余弦值;
的的余弦值;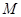 是线段
是线段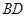 上一动点,试确定
上一动点,试确定 ,并证明你的结论.
,并证明你的结论.
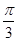 ,D、E分别为AA1、A1C的中点.
,D、E分别为AA1、A1C的中点.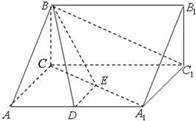
 的棱长为
的棱长为 ,点
,点 为
为 的中点.
的中点.