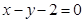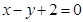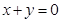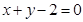题目内容
求直线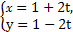 (t为参数)被圆
(t为参数)被圆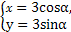 (α为参数)截得的弦长.
(α为参数)截得的弦长.
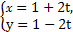 (t为参数)被圆
(t为参数)被圆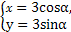 (α为参数)截得的弦长.
(α为参数)截得的弦长.2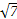
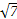
设圆的半径为R,直线被圆截得的弦长为L,
把直线方程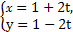 化为普通方程为x+y=2.
化为普通方程为x+y=2.
将圆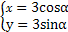 化为普通方程为x2+y2=9.
化为普通方程为x2+y2=9.
圆心O到直线的距离d=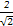 =
=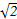 ,
,
所以弦长L=2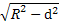 =2
=2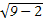 =2
=2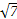 .
.
所以直线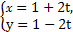 ,被圆
,被圆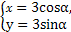 截得的弦长为2
截得的弦长为2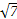 .
.
把直线方程
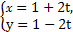 化为普通方程为x+y=2.
化为普通方程为x+y=2.将圆
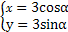 化为普通方程为x2+y2=9.
化为普通方程为x2+y2=9.圆心O到直线的距离d=
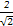 =
=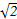 ,
,所以弦长L=2
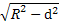 =2
=2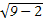 =2
=2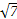 .
.所以直线
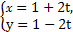 ,被圆
,被圆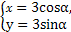 截得的弦长为2
截得的弦长为2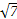 .
.
练习册系列答案
相关题目
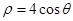 ,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是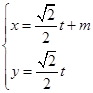 (t是参数)
(t是参数)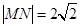 ,求实数m的值.
,求实数m的值.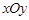 中,曲线
中,曲线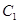 的参数方程为
的参数方程为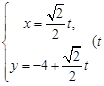 为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点
为参数).在极坐标系(与直角坐标取相同的长度单位,且以原点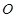 为极点,
为极点,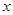 轴的非负半轴为极轴)中,曲线
轴的非负半轴为极轴)中,曲线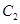 的方程为
的方程为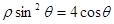 .
.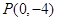 ,求
,求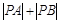 的值.
的值.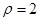 上的点到直线
上的点到直线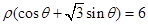 的距离的最小值为________.
的距离的最小值为________.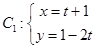 (t为参数)与曲线
(t为参数)与曲线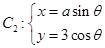 (
(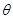 为参数,
为参数,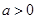 )有一个公共点在x轴上,则
)有一个公共点在x轴上,则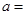 .
.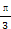 )且和极轴成
)且和极轴成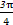 角的直线.
角的直线.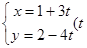 为参数),则直线L的倾斜角的余弦值为( )
为参数),则直线L的倾斜角的余弦值为( )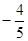
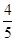
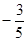
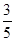
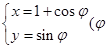 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.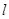 的极坐标方程是
的极坐标方程是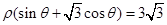 ,射线
,射线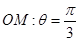 与圆C的交点为O,P与直线
与圆C的交点为O,P与直线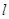 的参数方程为
的参数方程为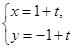 (
(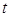 为参数),则直线
为参数),则直线