题目内容
如图①,正三角形ABC边长2,CD为AB边上的高,E、F分别为AC、BC中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图②(1)判断翻折后直线AB与面DEF的位置关系,并说明理由
(2)求二面角B-AC-D的余弦值
(3)求点C到面DEF的距离
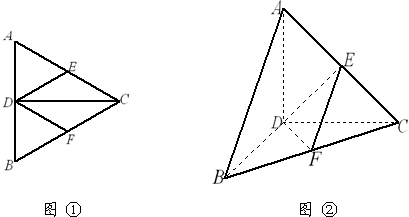
分析:(1)由已知中E、F分别为AC、BC中点,由三角形中位线定理可得EF∥AB,由线面平行的判定定理可得AB∥平面DEF
(2)过D作DH垂直AC于H,连接HB,根据二面角的平面角可得∠BDH是B-AC-D的二面角的平面角,解三角形BDH,即可得到二面角B-AC-D的余弦值
(3)过点E作FK垂直CD于K,可证得FK是三棱锥C-DEF的高,由此我们计算出三棱锥C-DEF的体积,和S△DEF利用等体积法,即可得到点C到面DEF的距离.
(2)过D作DH垂直AC于H,连接HB,根据二面角的平面角可得∠BDH是B-AC-D的二面角的平面角,解三角形BDH,即可得到二面角B-AC-D的余弦值
(3)过点E作FK垂直CD于K,可证得FK是三棱锥C-DEF的高,由此我们计算出三棱锥C-DEF的体积,和S△DEF利用等体积法,即可得到点C到面DEF的距离.
解答: 解:(1)在三角形ABC中,EF是中位线,所以EF∥AB
解:(1)在三角形ABC中,EF是中位线,所以EF∥AB
EF属于平面DEF里,且直线AB不属于平面DEF,
∴AB∥平面DEF
(2)过D作DH垂直AC于H,连接HB
BD垂直于AD,BD垂直于CD,
又因为AD和CD相交于点D,
∴所以BD垂直于平面ACD
AC属于平面ACD,所以BD垂直于AC
又因为DH垂直于AC
所以∠BDH是B-AC-D的二面角
在三角形BDH里,∠BDH是直角(因为BD垂直于平面ACD,所以BD垂直于DH)
BD=1
DH=AD•sin60°=
tan∠BHD=
=
cos∠BHD=
(3)求三棱锥C-DEF的体积
过点E作FK垂直CD于K,
在三角形BCD中,FK是中位线,FK∥BD,且FK=
BD=
又BD垂直于平面ACD,可知FK垂直于平面ACD
即FK垂直于平面ECD
所以FK是三棱锥C-DEF的高
S△CED=
VC-DEF=
又∵S△DEF=
∴点C到面DEF的距离为
 解:(1)在三角形ABC中,EF是中位线,所以EF∥AB
解:(1)在三角形ABC中,EF是中位线,所以EF∥ABEF属于平面DEF里,且直线AB不属于平面DEF,
∴AB∥平面DEF
(2)过D作DH垂直AC于H,连接HB
BD垂直于AD,BD垂直于CD,
又因为AD和CD相交于点D,
∴所以BD垂直于平面ACD
AC属于平面ACD,所以BD垂直于AC
又因为DH垂直于AC
所以∠BDH是B-AC-D的二面角
在三角形BDH里,∠BDH是直角(因为BD垂直于平面ACD,所以BD垂直于DH)
BD=1
DH=AD•sin60°=
| ||
| 2 |
tan∠BHD=
| BD |
| DH |
2
| ||
| 3 |
cos∠BHD=
| ||
| 7 |
(3)求三棱锥C-DEF的体积
过点E作FK垂直CD于K,
在三角形BCD中,FK是中位线,FK∥BD,且FK=
| 1 |
| 2 |
| 1 |
| 2 |
又BD垂直于平面ACD,可知FK垂直于平面ACD
即FK垂直于平面ECD
所以FK是三棱锥C-DEF的高
S△CED=
| ||
| 4 |
VC-DEF=
| ||
| 24 |
又∵S△DEF=
| ||
| 8 |
∴点C到面DEF的距离为
| ||
| 7 |
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,点到平面的距离,其中(1)的关键是证得EF∥AB,(2)的关键是证得∠BDH是B-AC-D的二面角的平面角,(3)的关键是利用等体积法进行解答.

练习册系列答案
相关题目
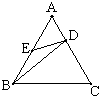 如图,在正三角形ABC中,D、E分别在AC、AB上,
如图,在正三角形ABC中,D、E分别在AC、AB上,| AD |
| AC |
| 1 |
| 3 |
| A、△AED∽△BED |
| B、△AED∽△CBD |
| C、△AED∽△ABD |
| D、△BAD∽△BCD |
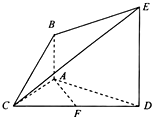 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.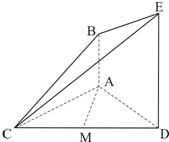 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB.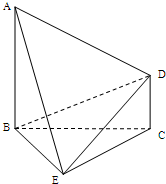 如图,已知AB⊥平面BCE,CD∥ab,△BCE是正三角形,AB=BC=2CD.
如图,已知AB⊥平面BCE,CD∥ab,△BCE是正三角形,AB=BC=2CD. 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.