题目内容
 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.(Ⅰ)求证:AF∥平面BCE;
(Ⅱ)求证:平面BCE⊥平面CDE;
(Ⅲ)设平面BCE∩平面ACD=l,试问直线l是否和平面ABED平行,说明理由.
分析:(I)取CE中点P,连接FP,BP,根据三角形中位线性质,我们易得四边形ABPF为平行四边形,则AF∥BP,再由线面平行的判定定理可得AM∥平面BCE;
(Ⅱ)先利用线面垂直的判定定理证明AF⊥平面DCE,再利用面面垂直的判定定理证明平面BCE⊥平面CDE;
(Ⅲ)假设直线l和平面ABED平行,利用线面平行的性质,可得AD∥EB,与AD,EB相交矛盾,故可得结论.
(Ⅱ)先利用线面垂直的判定定理证明AF⊥平面DCE,再利用面面垂直的判定定理证明平面BCE⊥平面CDE;
(Ⅲ)假设直线l和平面ABED平行,利用线面平行的性质,可得AD∥EB,与AD,EB相交矛盾,故可得结论.
解答: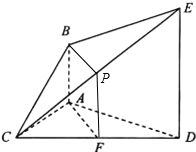 (I)证明:取CE中点P,连接FP,BP
(I)证明:取CE中点P,连接FP,BP
∵F是CD的中点,
∴FP∥DE且FP=
DE
∵AB∥DE,AB=
DE
∴AB∥FP,AB=FP
∴四边形ABPF为平行四边形
∴AF∥BP
∵AF?平面BCE,BP?平面BCE
∴AM∥平面BCE;
(Ⅱ)证明:∵△ACD是正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE∥AB
∴DE⊥平面ACD,
∵AF?平面ACD,
∴DE⊥AF
∵CD∩DE=D
∴AF⊥平面DCE
∵BP∥AF,
∴BP⊥平面DCE
∵BP?平面BCE
∴平面BCE⊥平面CDE;
(Ⅲ)解:假设直线l和平面ABED平行
∵l?平面BCE,平面BCE∩平面ABED=EB
∴l∥EB
同理l∥AD
∴AD∥EB,与AD,EB相交矛盾
∴直线l和平面ABED不平行.
 (I)证明:取CE中点P,连接FP,BP
(I)证明:取CE中点P,连接FP,BP∵F是CD的中点,
∴FP∥DE且FP=
| 1 |
| 2 |
∵AB∥DE,AB=
| 1 |
| 2 |
∴AB∥FP,AB=FP
∴四边形ABPF为平行四边形
∴AF∥BP
∵AF?平面BCE,BP?平面BCE
∴AM∥平面BCE;
(Ⅱ)证明:∵△ACD是正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE∥AB
∴DE⊥平面ACD,
∵AF?平面ACD,
∴DE⊥AF
∵CD∩DE=D
∴AF⊥平面DCE
∵BP∥AF,
∴BP⊥平面DCE
∵BP?平面BCE
∴平面BCE⊥平面CDE;
(Ⅲ)解:假设直线l和平面ABED平行
∵l?平面BCE,平面BCE∩平面ABED=EB
∴l∥EB
同理l∥AD
∴AD∥EB,与AD,EB相交矛盾
∴直线l和平面ABED不平行.
点评:本题考查线面平行的判定与性质,考查线面垂直、面面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.