题目内容
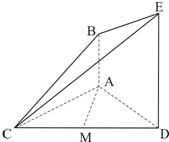 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB.(1)设M是线段CD的中点,求证:AM∥平面BCE;
(2)求直线CB与平面ABED所成角的余弦值.
分析:(I)取CE中点N,连接MN,BN,根据三角形中位线性质,我们易得四边形ABNM为平行四边形,则AM∥BN,再由线面平行的判定定理可得AM∥平面BCE.
(II)取AD中点H,连接BH,结合正三角形的性质,及线面垂直的性质,由已知中AB⊥平面ACD,△ACD是正三角形,我们可由线面垂直的判定定理得到CH⊥平面ABED,则∠CBH为直线 CB与平面ABED所成的角,解三角形CBH即可得到答案.
(II)取AD中点H,连接BH,结合正三角形的性质,及线面垂直的性质,由已知中AB⊥平面ACD,△ACD是正三角形,我们可由线面垂直的判定定理得到CH⊥平面ABED,则∠CBH为直线 CB与平面ABED所成的角,解三角形CBH即可得到答案.
解答: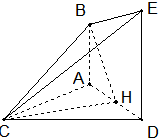 证明:(I)取CE中点N,连接MN,BN
证明:(I)取CE中点N,连接MN,BN
则MN∥DE∥AB且MN=
DE=AB
∴四边形ABNM为平行四边形∴AM∥BN …(4分)
∴AM∥平面BCE …(6分)
解:(Ⅱ)取AD中点H,连接BH,
∵△ACD是正三角形,∴CH⊥AD …(8分)
又∵AB⊥平面ACD∴CH⊥AB
∴CH⊥平面ABED…(10分)
∴∠CBH为直线 CB与平面ABED所成的角…(12分)
设AB=a,则AC=AD=2a,∴BH=
a BC=
a
cos∠CBH=
=
=
…(14分)
 证明:(I)取CE中点N,连接MN,BN
证明:(I)取CE中点N,连接MN,BN则MN∥DE∥AB且MN=
| 1 |
| 2 |
∴四边形ABNM为平行四边形∴AM∥BN …(4分)
∴AM∥平面BCE …(6分)
解:(Ⅱ)取AD中点H,连接BH,
∵△ACD是正三角形,∴CH⊥AD …(8分)
又∵AB⊥平面ACD∴CH⊥AB
∴CH⊥平面ABED…(10分)
∴∠CBH为直线 CB与平面ABED所成的角…(12分)
设AB=a,则AC=AD=2a,∴BH=
| 2 |
| 5 |
cos∠CBH=
| BH |
| BC |
| ||
|
| ||
| 5 |
点评:本题考查的知识点是直线与平面所成的角,直线与平面平行的判定,其中(1)的关键是得到AM∥BN,(2)的关键是得到∠CBH为直线 CB与平面ABED所成的角.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 (2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•惠州模拟)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(2012•枣庄一模)如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点. 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD为等边三角形,AD=DE=2AB,F为CD的中点 如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,且AC=AD=DE=2AB=4,F为CD的中点.